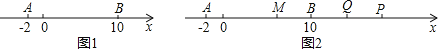题目内容
【题目】如图,数轴上标出的所有点中,任意相邻两点间的距离相等,已知点A表示﹣12,点G表示6.
![]()
(1)表示原点的点是 ,点C表示的数是 ;
(2)数轴上有两点M、N,点M到点D的距离为![]() ,点N到点D的距离为4,求点M,N之间的距离;
,点N到点D的距离为4,求点M,N之间的距离;
(3)点P为数轴上一点,且表示的数是整数,点P到点A的距离与点P到点G的距离之和为18,则这样的点P有 个.
【答案】(1)点E,﹣6(2)点M,N之间的距离为4﹣![]() 或4+
或4+![]() ;(3)19.
;(3)19.
【解析】
(1)点A表示﹣12,点G表示6,可求出AG的长,除以6可得每段的长,从而可得原点及点C表示的数;
(2)由(1)及已知条件可得点D表示的数,根据点M到点D的距离为![]() ,点N到点D的距离为4,可求得点M与点N表示的数,再由数轴上右边的数总比左边的大,用右边的数减去左边的数,可得MN的值;
,点N到点D的距离为4,可求得点M与点N表示的数,再由数轴上右边的数总比左边的大,用右边的数减去左边的数,可得MN的值;
(3)AG=6﹣(﹣12)=18,点P到点A的距离与点P到点G的距离之和为18,问题可解.
解:(1)∵点A表示﹣12,点G表示6
∴AG=6﹣(﹣12)=18
∵数轴上标出的所有点中,任意相邻两点间的距离相等
∴18÷6=3
∴相邻两点间的距离为3
∴6﹣2×3=0,﹣12+3×2=﹣6
表示原点的点是点E,点C表示的数是﹣6.
故答案为:点E,﹣6.
(2)∵点D表示的数为﹣3,点M到点D的距离为![]() ,点N到点D的距离为4
,点N到点D的距离为4
点M表示的数为:﹣3﹣![]() 或﹣3+
或﹣3+![]() ,
,
点N表示的数为:﹣7或1
∴点M,N之间的距离为:
①﹣3﹣![]() ﹣(﹣7)=4﹣
﹣(﹣7)=4﹣![]() ,
,
②﹣3+![]() ﹣(﹣7)=4+
﹣(﹣7)=4+![]() ,
,
③1﹣(﹣3﹣![]() )=4+
)=4+![]() ,
,
④1﹣(﹣3+![]() )=4﹣
)=4﹣![]() ,
,
∴综上可得点M,N之间的距离为=4﹣![]() 或4+
或4+![]() .
.
(3)∵AG=6﹣(﹣12)=18,点P到点A的距离与点P到点G的距离之和为18
∴P为AG之间的所有整数,共有19个
故答案为:19.

 名校课堂系列答案
名校课堂系列答案