题目内容
【题目】如图,点A是反比例函数![]() (x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数
(x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数![]() (k<0,x<0)的图象于点B,且S△AOB=5.
(k<0,x<0)的图象于点B,且S△AOB=5.
(1) k的值为_______;
(2) 若点A的横坐标是1,
①求∠AOB的度数;
②在y2的图象上找一点P(异于点B), 使S△AOP=S△AOB,求点P的坐标.

【答案】-8
【解析】试题分析:(1)首先设AB交y轴于点C,由点A是反比例函数![]() (x>0)图象上的任意一点,AB∥x轴,根据反比例函数系数
(x>0)图象上的任意一点,AB∥x轴,根据反比例函数系数![]() 的几何意义求得
的几何意义求得![]() 的面积,又由
的面积,又由![]() 的面积等于5,可求得
的面积等于5,可求得![]() 的面积,继而求得
的面积,继而求得![]() 的值;
的值;
(2)①由点A的横坐标是1,可求得点A的坐标,继而求得点![]() 的纵坐标,则可求得点
的纵坐标,则可求得点![]() 的坐标,则可求得
的坐标,则可求得![]() 的长,然后由勾股定理的逆定理,求得
的长,然后由勾股定理的逆定理,求得![]() 的度数;
的度数;
②过点A作AM⊥x轴于点A,过点P作PN⊥x轴于点N,设![]() 根据反比例函数系数k的几何意义得出
根据反比例函数系数k的几何意义得出![]() 由S△AOP=S△梯形APNMS△NOPS△AOM=S△AOB=5,列出方程
由S△AOP=S△梯形APNMS△NOPS△AOM=S△AOB=5,列出方程![]()
解方程即可.
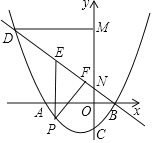
试题解析:(1)如图1,设AB交y轴于点C,
∵点A是反比例函数![]() (x>0)图象上的任意一点,且AB∥x轴,
(x>0)图象上的任意一点,且AB∥x轴,
∴AB⊥y轴,
![]()
![]()
∴![]()
∵反比例函数![]() (k<0,x<0)的图象过点B,AB⊥y轴,
(k<0,x<0)的图象过点B,AB⊥y轴,
![]()
∴k=8;
故答案为:8;
(2)①∵点A的横坐标是1,
![]()
∴点A(1,2),
∵AB∥x轴,
∴点B的纵坐标为2,
![]()
解得:x=4,
∴点B(4,2),
![]() ∴
∴![]()
![]()
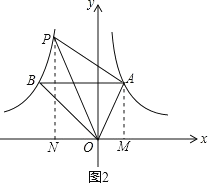
②如图2,过点A作AM⊥x轴于点A,过点P作PN⊥x轴于点N,设![]()
则![]()
∵S△AOP=S△梯形APNMS△NOPS△AOM=S△AOB=5,
![]()
整理,得![]()
解得![]() (不合题意舍去),
(不合题意舍去),
∴点P的坐标为(1,8).

练习册系列答案
相关题目