ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΈ ΧβΧα≥ω
![]() »γΆΦ1Θ§ΒψAΈΣœΏΕΈBCΆβ“ΜΕ·ΒψΘ§«“
»γΆΦ1Θ§ΒψAΈΣœΏΕΈBCΆβ“ΜΕ·ΒψΘ§«“![]() Θ§ΧνΩ’ΘΚΒ±ΒψAΈΜ”Ύ______ ±Θ§œΏΕΈACΒΡ≥Λ»ΓΒΟΉν¥σ÷ΒΘ§«“Ήν¥σ÷ΒΈΣ______
Θ§ΧνΩ’ΘΚΒ±ΒψAΈΜ”Ύ______ ±Θ§œΏΕΈACΒΡ≥Λ»ΓΒΟΉν¥σ÷ΒΘ§«“Ήν¥σ÷ΒΈΣ______![]() ”ΟΚ§
”ΟΚ§![]() ΒΡ ΫΉ”±μ Ψ
ΒΡ ΫΉ”±μ Ψ![]() Θ°
Θ°
Έ ΧβΧΫΨΩ
![]() ΒψAΈΣœΏΕΈBCΆβ“ΜΕ·ΒψΘ§«“
ΒψAΈΣœΏΕΈBCΆβ“ΜΕ·ΒψΘ§«“![]() Θ§»γΆΦ2Υυ ΨΘ§Ζ÷±π“‘
Θ§»γΆΦ2Υυ ΨΘ§Ζ÷±π“‘![]() ΈΣ±ΏΘ§ΉςΒ»±Ώ»ΐΫ«–ΈABDΚΆΒ»±Ώ»ΐΫ«–ΈACEΘ§Ν§Ϋ”
ΈΣ±ΏΘ§ΉςΒ»±Ώ»ΐΫ«–ΈABDΚΆΒ»±Ώ»ΐΫ«–ΈACEΘ§Ν§Ϋ”![]() Θ§’“≥ωΆΦ÷–”κBEœύΒ»ΒΡœΏΕΈΘ§«κΥΒΟςάμ”…Θ§≤Δ÷±Ϋ”–¥≥ωœΏΕΈBE≥ΛΒΡΉν¥σ÷ΒΘ°
Θ§’“≥ωΆΦ÷–”κBEœύΒ»ΒΡœΏΕΈΘ§«κΥΒΟςάμ”…Θ§≤Δ÷±Ϋ”–¥≥ωœΏΕΈBE≥ΛΒΡΉν¥σ÷ΒΘ°
Έ ΧβΫβΨωΘΚ
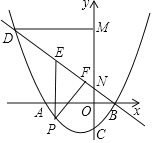
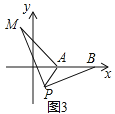
![]() »γΆΦ3Θ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΒψAΒΡΉχ±ξΈΣ
»γΆΦ3Θ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΒψAΒΡΉχ±ξΈΣ![]() Θ§ΒψBΒΡΉχ±ξΈΣ
Θ§ΒψBΒΡΉχ±ξΈΣ![]() Θ§ΒψPΈΣœΏΕΈABΆβ“ΜΕ·ΒψΘ§«“
Θ§ΒψPΈΣœΏΕΈABΆβ“ΜΕ·ΒψΘ§«“![]() Θ§«σœΏΕΈAM≥ΛΒΡΉν¥σ÷ΒΦΑ¥Υ ±ΒψPΒΡΉχ±ξΘ°
Θ§«σœΏΕΈAM≥ΛΒΡΉν¥σ÷ΒΦΑ¥Υ ±ΒψPΒΡΉχ±ξΘ°
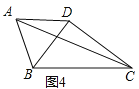
![]() »γΆΦ4Θ§‘ΎΥΡ±Ώ–ΈABCD÷–Θ§
»γΆΦ4Θ§‘ΎΥΡ±Ώ–ΈABCD÷–Θ§ ![]() Θ§»τΕ‘Ϋ«œΏ
Θ§»τΕ‘Ϋ«œΏ![]() ”ΎΒψDΘ§«κ÷±Ϋ”–¥≥ωΕ‘Ϋ«œΏACΒΡΉν¥σ÷ΒΘ°
”ΎΒψDΘ§«κ÷±Ϋ”–¥≥ωΕ‘Ϋ«œΏACΒΡΉν¥σ÷ΒΘ°

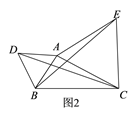
ΓΨ¥πΑΗΓΩ CBΒΡ―”≥ΛœΏ…œΘΜ ![]()
ΓΨΫβΈωΓΩΖ÷ΈωΘΚ
Θ®1Θ©”…Χβ“βΩ…÷ΣΘ§Β±ΒψA‘ΎCBΒΡ―”≥ΛœΏ…œ ±Θ§œΏΕΈACΒΡ÷ΒΉν¥σΘ§Ήν¥σ÷ΒΈΣΘΚAC=AB+BC=a+bΘΜ
Θ®2Θ©”…“―÷ΣΧθΦΰ“Ή÷ΛΓςABEΓ’ΓςADCΘ§”…¥ΥΩ…ΒΟBE=DCΘ§ΫαΚœΘ®1Θ©÷–Ϋα¬έΩ…÷ΣΘ§Β±ΒψD‘ΎCBΒΡ―”≥ΛœΏ…œ ±Θ§BEΉν≥Λ=CDΉν≥Λ=BC+AB=9ΘΜ
Θ®3Θ©ΔΌ»γœ¬ΆΦ5Θ§Ν§Ϋ”BMΘ§ΫΪΓςAPM»ΤΉ≈ΒψPΥ≥ ±’κ–ΐΉΣ![]() ΒΟΒΫΓςPBNΘ§Ν§Ϋ”ANΘ§‘ρΓςAPN «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρ”…“―÷Σ“ΉΒΟAB=3Θ§AN=
ΒΟΒΫΓςPBNΘ§Ν§Ϋ”ANΘ§‘ρΓςAPN «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρ”…“―÷Σ“ΉΒΟAB=3Θ§AN=![]() AP=
AP=![]() Θ§ΫαΚœΘ®1Θ©Ω…÷ΣΘ§Β±ΒψN‘ΎBAΒΡ―”≥ΛœΏ…œ ±Θ§AMΉν¥σ=BNΉν¥σ=AB+AN=
Θ§ΫαΚœΘ®1Θ©Ω…÷ΣΘ§Β±ΒψN‘ΎBAΒΡ―”≥ΛœΏ…œ ±Θ§AMΉν¥σ=BNΉν¥σ=AB+AN=![]() ΘΜ»γΆΦ6Θ§Β±ΒψN‘ΎBAΒΡ―”≥ΛœΏ…œ ±Θ§ΙΐΒψPΉςPEΓΆAN”ΎΒψEΘ§”…ΓςAPN «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§AP=2Θ§Φ¥Ω…«σΒΟOEΚΆPEΒΡ≥ΛΘ§¥”ΕχΩ…ΒΟ¥Υ ±ΒψPΒΡΉχ±ξΘΜΔΎ»γœ¬ΆΦ7Θ§“‘BCΈΣ±ΏΉςΒ»±Ώ»ΐΫ«–ΈΓςBCMΘ§Ν§Ϋ”DMΘ§”…“―÷ΣΧθΦΰ“Ή÷ΛΓςABCΓ’ΓςDBMΘ§¥”ΕχΩ…ΒΟAC=DMΘ§”…¥ΥΩ…ΒΟΒ±DMΒΡ÷ΒΉν¥σ ±Θ§ACΒΡ÷ΒΨΆΉν¥σΘ§”…ΓœBDC=90ΓψΩ…÷ΣΒψD‘Ύ“‘BCΈΣ÷±ΨΕΒΡ
ΘΜ»γΆΦ6Θ§Β±ΒψN‘ΎBAΒΡ―”≥ΛœΏ…œ ±Θ§ΙΐΒψPΉςPEΓΆAN”ΎΒψEΘ§”…ΓςAPN «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§AP=2Θ§Φ¥Ω…«σΒΟOEΚΆPEΒΡ≥ΛΘ§¥”ΕχΩ…ΒΟ¥Υ ±ΒψPΒΡΉχ±ξΘΜΔΎ»γœ¬ΆΦ7Θ§“‘BCΈΣ±ΏΉςΒ»±Ώ»ΐΫ«–ΈΓςBCMΘ§Ν§Ϋ”DMΘ§”…“―÷ΣΧθΦΰ“Ή÷ΛΓςABCΓ’ΓςDBMΘ§¥”ΕχΩ…ΒΟAC=DMΘ§”…¥ΥΩ…ΒΟΒ±DMΒΡ÷ΒΉν¥σ ±Θ§ACΒΡ÷ΒΨΆΉν¥σΘ§”…ΓœBDC=90ΓψΩ…÷ΣΒψD‘Ύ“‘BCΈΣ÷±ΨΕΒΡ![]() …œ‘ΥΕ·Θ§”…ΆΦΩ…÷ΣΒ±D‘ΎBC…œΖΫΘ§«“DMΓΆBC ±Θ§DMΒΡ÷ΒΉν¥σΘ§Ήν¥σ÷ΒΈΣΘΚΒ»―ϋ÷±Ϋ«ΓςBDC–±±ΏBC…œΒΡΗΏ+Β»±ΏΓςBMCΒΡΗΏ.
…œ‘ΥΕ·Θ§”…ΆΦΩ…÷ΣΒ±D‘ΎBC…œΖΫΘ§«“DMΓΆBC ±Θ§DMΒΡ÷ΒΉν¥σΘ§Ήν¥σ÷ΒΈΣΘΚΒ»―ϋ÷±Ϋ«ΓςBDC–±±ΏBC…œΒΡΗΏ+Β»±ΏΓςBMCΒΡΗΏ.
œξΫβΘΚ
Θ®1Θ©ΓΏΒψAΈΣœΏΕΈBCΆβ“ΜΕ·ΒψΘ§«“![]() Θ§
Θ§
ΓύΒ±ΒψAΈΜ”ΎCBΒΡ―”≥ΛœΏ…œ ±Θ§œΏΕΈACΒΡ≥Λ»ΓΒΟΉν¥σ÷ΒΘ§«“Ήν¥σ÷ΒΈΣ![]() Θ§
Θ§
Ι ¥πΑΗΈΣΘΚCBΒΡ―”≥ΛœΏ…œΘ§ ![]() ΘΜ
ΘΜ
![]() Θ§
Θ§
άμ”…ΘΚΓΏ![]() ”κ
”κ![]() «Β»±Ώ»ΐΫ«–ΈΘ§
«Β»±Ώ»ΐΫ«–ΈΘ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Φ¥![]() Θ§
Θ§
‘Ύ![]() ”κ
”κ![]() ÷–Θ§
÷–Θ§
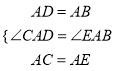 Θ§
Θ§
Γύ![]() Γ’
Γ’![]() Θ§
Θ§
Γύ![]() ΘΜ
ΘΜ
ΔΎΓΏœΏΕΈBE≥ΛΒΡΉν¥σ÷Β![]() œΏΕΈCDΒΡΉν¥σ÷ΒΘ§
œΏΕΈCDΒΡΉν¥σ÷ΒΘ§
Γύ”…![]() ÷ΣΘ§Β±œΏΕΈCDΒΡ≥Λ»ΓΒΟΉν¥σ÷Β ±Θ§ΒψD‘ΎCBΒΡ―”≥ΛœΏ…œΘ§
÷ΣΘ§Β±œΏΕΈCDΒΡ≥Λ»ΓΒΟΉν¥σ÷Β ±Θ§ΒψD‘ΎCBΒΡ―”≥ΛœΏ…œΘ§
ΓύΉν¥σ÷ΒΈΣ![]() ΘΜ
ΘΜ
Θ®3Θ©ΔΌ»γΆΦ5Θ§Ν§Ϋ”BMΘ§ΫΪ![]() »ΤΉ≈ΒψPΥ≥ ±’κ–ΐΉΣ
»ΤΉ≈ΒψPΥ≥ ±’κ–ΐΉΣ![]() ΒΟΒΫ
ΒΟΒΫ![]() Θ§Ν§Ϋ”ANΘ§‘ρ
Θ§Ν§Ϋ”ANΘ§‘ρ![]() «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
«Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
Γύ![]() Θ§
Θ§
ΓΏ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§ΒψBΒΡΉχ±ξΈΣ
Θ§ΒψBΒΡΉχ±ξΈΣ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύœΏΕΈAM≥ΛΒΡΉν¥σ÷Β![]() œΏΕΈBN≥ΛΒΡΉν¥σ÷ΒΘ§
œΏΕΈBN≥ΛΒΡΉν¥σ÷ΒΘ§
ΓύΒ±N‘ΎœΏΕΈBAΒΡ―”≥ΛœΏ ±Θ§œΏΕΈBN»ΓΒΟΉν¥σ÷ΒΘ§
Ήν¥σ÷Β![]() Θ§
Θ§
ΓΏ![]() Θ§
Θ§
ΓύΉν¥σ÷ΒΈΣ![]() ΘΜ
ΘΜ
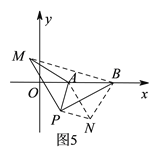
»γΆΦ6Θ§ΙΐPΉς![]() ÷α”ΎEΘ§
÷α”ΎEΘ§
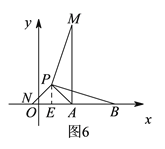
ΓΏ![]() «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
«Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ![]()
ΔΎ»γœ¬ΆΦ7Θ§“‘BCΈΣ±ΏΉςΒ»±Ώ»ΐΫ«–ΈΓςBCMΘ§Ν§Ϋ”DMΘ§
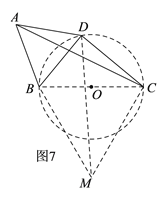
ΓΏ![]() Θ§
Θ§
Γύ![]()
ΓΏ![]() Θ§
Θ§
Γύ![]() Γ’
Γ’![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ”ϊ«σACΒΡΉν¥σ÷ΒΘ§÷Μ“Σ«σ≥ωDMΒΡΉν¥σ÷ΒΦ¥Ω…Θ§
ΓΏ![]() Ε®÷ΒΘ§
Ε®÷ΒΘ§ ![]() Θ§
Θ§
ΓύΒψD‘Ύ“‘BCΈΣ÷±ΨΕΒΡ![]() …œ‘ΥΕ·Θ§
…œ‘ΥΕ·Θ§
”…ΆΦœσΩ…÷ΣΘ§Β±ΒψD‘ΎBC…œΖΫΘ§DMΓΆBC ±Θ§DMΒΡ÷ΒΉν¥σΘ§Ήν¥σ÷Β=Β»―ϋ÷±Ϋ«ΓςBDC–±±Ώ…œΒΡΗΏ+Β»±ΏΓςBCMΒΡΗΏΘ§
ΓΏBC=![]() Θ§
Θ§
ΓύDMΉν¥σ=![]() Θ§
Θ§
ΓύACΉν¥σ=![]() Θ°
Θ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
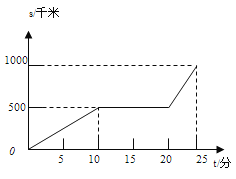
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΡ≥…Χ≥ΓΨ≠”ΣΡ≥÷÷ΤΖ≈ΤΒΡΆφΨΏΘ§ΙΚΫχ ±ΒΡΒΞΦέ «30‘ΣΘ§ΗυΨί –≥ΓΒς≤ιΘΚ‘Ύ“ΜΕΈ ±ΦδΡΎΘ§œζ έΒΞΦέ «40‘Σ ±Θ§œζ έΝΩ «600ΦΰΘ§Εχœζ έΒΞΦέΟΩ’«1‘ΣΘ§ΨΆΜα…Ό έ≥ω10ΦΰΆφΨΏΘ°
![]() ≤ΜΖΝ…ηΗΟ÷÷ΤΖ≈ΤΆφΨΏΒΡœζ έΒΞΦέΈΣx‘Σ
≤ΜΖΝ…ηΗΟ÷÷ΤΖ≈ΤΆφΨΏΒΡœζ έΒΞΦέΈΣx‘Σ![]() Θ§«κΡψΖ÷±π”ΟxΒΡ¥ζ ΐ Ϋά¥±μ Ψœζ έΝΩyΦΰΚΆœζ έΗΟΤΖ≈ΤΆφΨΏΜώΒΟάϊ»σw‘ΣΘ§≤ΔΑ―ΫαΙϊΧν–¥‘Ύ±μΗώ÷–ΘΚ
Θ§«κΡψΖ÷±π”ΟxΒΡ¥ζ ΐ Ϋά¥±μ Ψœζ έΝΩyΦΰΚΆœζ έΗΟΤΖ≈ΤΆφΨΏΜώΒΟάϊ»σw‘ΣΘ§≤ΔΑ―ΫαΙϊΧν–¥‘Ύ±μΗώ÷–ΘΚ
œζ έΒΞΦέ | x |
œζ έΝΩ | ______ |
œζ έΆφΨΏΜώΒΟάϊ»σ | ______ |
![]() ‘Ύ
‘Ύ![]() Έ ΧθΦΰœ¬Θ§»τ…Χ≥ΓΜώΒΟΝΥ10000‘Σœζ έάϊ»σΘ§«σΗΟΆφΨΏœζ έΒΞΦέx”ΠΕ®ΈΣΕύ…Ό‘ΣΘ°
Έ ΧθΦΰœ¬Θ§»τ…Χ≥ΓΜώΒΟΝΥ10000‘Σœζ έάϊ»σΘ§«σΗΟΆφΨΏœζ έΒΞΦέx”ΠΕ®ΈΣΕύ…Ό‘ΣΘ°
![]() ‘Ύ
‘Ύ![]() Έ ΧθΦΰœ¬Θ§»τΆφΨΏ≥ßΙφΕ®ΗΟΤΖ≈ΤΆφΨΏœζ έΒΞΦέ≤ΜΒΆ”Ύ44‘ΣΘ§«“…Χ≥Γ“ΣΆξ≥…≤Μ…Ό”Ύ540ΦΰΒΡœζ έ»ΈΈώΘ§«σ…Χ≥Γœζ έΗΟΤΖ≈ΤΆφΨΏΜώΒΟΒΡΉν¥σάϊ»σ «Εύ…ΌΘΩ
Έ ΧθΦΰœ¬Θ§»τΆφΨΏ≥ßΙφΕ®ΗΟΤΖ≈ΤΆφΨΏœζ έΒΞΦέ≤ΜΒΆ”Ύ44‘ΣΘ§«“…Χ≥Γ“ΣΆξ≥…≤Μ…Ό”Ύ540ΦΰΒΡœζ έ»ΈΈώΘ§«σ…Χ≥Γœζ έΗΟΤΖ≈ΤΆφΨΏΜώΒΟΒΡΉν¥σάϊ»σ «Εύ…ΌΘΩ