题目内容
【题目】根据你的经验,分别求下列事件的概率:
(1)在一个不透明的袋中装有红球3个,白球2个,黑球1个,每种球除颜色外其余都相同,摇匀后随机地从袋中取出1个球,取到红球的概率.
(2)投掷一枚普通正方体骰子,出现的点数为7的概率.
(3)投掷两枚普通硬币,出现两个正面的概率.
【答案】(1)取到红色球的概率为![]() ;(2)出现的点数为7的概率是0;(3)出现两个正面的概率为
;(2)出现的点数为7的概率是0;(3)出现两个正面的概率为![]() .
.
【解析】分析:(1)用红球的个数除以球的总个数可得;
(2)可判断该事件为不可能事件,其概率为0;
(3)列出所有等可能结果,根据概率公式求解可得.
详解:(1)∵袋子中共有6个球,其中红色球有3个,∴取到红色球的概率为![]() =
=![]() ;
;
(2)投掷一枚普通正方体骰子,不可能出现7点,∴出现的点数为7的概率是0;
(3)投掷两枚普通硬币,有4种情况:(正、正)、(正、反)、(反、正)、(反、反),出现两个正面只有一种情况,∴出现两个正面的概率为![]() .
.

练习册系列答案
相关题目
【题目】为了解“数学思想作为对学习数学帮助有多大?”一研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和下表来表示(图、表都没制作完成). 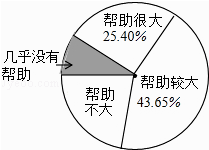
选项 | 帮助很大 | 帮助较大 | 帮助不大 | 几乎没有帮助 |
人数 | a | 543 | 269 | b |
根据图、表提供的信息.
(1)请问:这次共有多少名学生参与了问卷调查?
(2)算出表中a、b的值. (注:计算中涉及到的“人数”均精确到1)