Question

【题目】已知：在四边形ABCD中，根据下列不同条件求BD长．

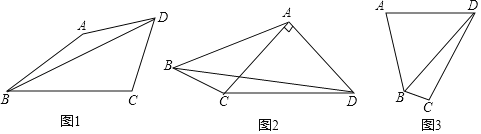
（1）如图1，当∠ABC＝∠ADC＝30°，AD＝DC，AB＝9，BC＝12时，求BD的长．

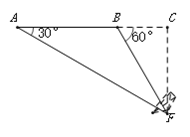
（2）如图2，当∠ABC＝∠ADC＝45°，AD⊥AC，AB＝6，BC＝5时，求BD的长．

（3）如图3，当∠ABC＝2∠ADC＝120°，AD＝DC，四边形ABCD的面积为4时，请直接写出BD的长是　 　．

Answer 1

【答案】(1)15;(2)13;(3)4.

【解析】

（1）如图1中，以AB为边向上作等边△ABE，连接BE，EC．证明BD=EC，求出EC即可解决问题．
（2）如图2中，作AF⊥AB，使得AF=AB，连接BF，CF．证明△FAC≌△BAD（SAS），推出CF=BD，利用勾股定理求出CF即可．
（3）如图3中，作DP⊥AB于P，DQ⊥BC于Q．证明S四边形ABCD=S△DPBQ=4，设BD=2x．则BP=BQ=x，DP=DQ=x，构建方程即可解决问题．

（1）如图1中，以AB为边向上作等边△ABE，连接BE，EC．

∵△DA＝DC，∠ADC＝60°，

∴△ADC是等边三角形，

∴∠EAB＝∠DAC＝60°，AE＝AB，AD＝AC，

∴∠EAC＝∠BAD，

∴△EAC≌△BAD（SAS），

∴BD＝EC，

∵∠ABC＝30°，∠ABE＝60°，

∴∠EBC＝90°，

∴EC＝，

∴BD＝EC＝15．

（2）如图2中，作AF⊥AB，使得AF＝AB，连接BF，CF．

∵AF＝AB，AC＝AD，∠BAF＝∠CAD，

∴∠CAF＝∠BAD，

∴△FAC≌△BAD（SAS），

∴CF＝BD，

∵∠FBA＝∠ABC＝45°，

∴∠FBC＝90°，

∵AB＝AF＝6，∠BAF＝90°，

∴BF＝AB＝12，

∴CF＝＝13，

∴BD＝FC＝13．

（3）如图3中，作DP⊥AB于P，DQ⊥BC于Q．

∵AD＝DC，∠ADC＝60°，

∴△ADC是等边三角形，

∴∠DAC＝∠DCA＝60°，

∵∠ABC+∠ADC＝180°，

∴A，B，C，D四点共圆，

∴∠ABD＝∠ACD＝60°，∠CBD＝∠CAD＝60°，

∴∠DBA＝∠DBC，

∵DP⊥BA，DQ⊥BC，

∴DP＝DQ，

∵∠DPB＝∠DQB＝90°，

∴Rt△ADP≌Rt△CDQ（HL），

∴S△ADP＝S△DCQ，

∴S四边形ABCD＝S△DPBQ＝4，

设BD＝2x．则BP＝BQ＝x，DP＝DQ＝x，

∴xx+xx＝4，

∴x＝2或﹣2（舍弃），

∴BD＝4，

故答案为4．