ƒøƒ⁄»ð
°æƒø°ø°æ‘ƒ∂¡¿ÌΩ‚°ø
»Ù![]() £¨
£¨ ![]() £¨
£¨ ![]() Œ™ ˝÷·…œ»˝µ„£¨»Ùµ„
Œ™ ˝÷·…œ»˝µ„£¨»Ùµ„![]() µΩ
µΩ![]() µƒæý¿Î «µ„
µƒæý¿Î «µ„![]() µΩ
µΩ![]() µƒæý¿Îµƒ
µƒæý¿Îµƒ![]() ±∂£¨Œ“√«æÕ≥∆µ„
±∂£¨Œ“√«æÕ≥∆µ„![]() «
«![]() µƒ”≈µ„£Æ¿˝»Á£¨»ÁÕº¢Ÿ£¨µ„
µƒ”≈µ„£Æ¿˝»Á£¨»ÁÕº¢Ÿ£¨µ„![]() ±Ì 浃 ˝Œ™
±Ì 浃 ˝Œ™![]() £¨µ„
£¨µ„![]() ±Ì 浃 ˝Œ™
±Ì 浃 ˝Œ™![]() £Æ±Ì æ ˝
£Æ±Ì æ ˝![]() µƒµ„
µƒµ„![]() µΩµ„
µΩµ„![]() µƒæý¿Î «
µƒæý¿Î «![]() £¨µΩµ„
£¨µΩµ„![]() µƒæý¿Î «
µƒæý¿Î «![]() £¨ƒ«√¥µ„
£¨ƒ«√¥µ„![]() «
«![]() µƒ”≈µ„£ª”÷»Á£¨±Ì æ
µƒ”≈µ„£ª”÷»Á£¨±Ì æ![]() µƒµ„
µƒµ„![]() µΩµ„
µΩµ„![]() µƒæý¿Î «
µƒæý¿Î «![]() £¨µΩµ„
£¨µΩµ„![]() µƒæý¿Î «
µƒæý¿Î «![]() £¨ƒ«√¥µ´µ„
£¨ƒ«√¥µ´µ„![]() «
«![]() µƒ∫√µ„£Æ
µƒ∫√µ„£Æ
°æ÷™ ∂‘À”√°ø
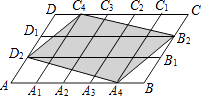
»ÁÕº¢⁄£¨![]() °¢
°¢![]() Œ™ ˝÷·…œ¡Ωµ„£¨µ„
Œ™ ˝÷·…œ¡Ωµ„£¨µ„![]() À˘±Ì 浃 ˝Œ™
À˘±Ì 浃 ˝Œ™![]() £¨µ„
£¨µ„![]() À˘±Ì 浃 ˝Œ™
À˘±Ì 浃 ˝Œ™![]() £Æ
£Æ
£®![]() £© ˝__________À˘±Ì 浃µ„ «
£© ˝__________À˘±Ì 浃µ„ «![]() µƒ”≈µ„£Æ
µƒ”≈µ„£Æ
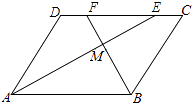
£®![]() £©»ÁÕº¢€£¨
£©»ÁÕº¢€£¨![]() £¨
£¨ ![]() Œ™ ˝÷·…œ¡Ωµ„£¨µ„
Œ™ ˝÷·…œ¡Ωµ„£¨µ„![]() À˘±Ì 浃 ˝Œ™
À˘±Ì 浃 ˝Œ™![]() £¨µ„
£¨µ„![]() À˘±Ì 浃 ˝Œ™
À˘±Ì 浃 ˝Œ™![]() £Æœ÷”–“ª÷ªµÁ◊”¬Ï“œ
£Æœ÷”–“ª÷ªµÁ◊”¬Ï“œ![]() ¥”µ„
¥”µ„![]() ≥ˆ∑¢£¨“‘
≥ˆ∑¢£¨“‘![]() ∏ˆµ•Œª√ø√εƒÀŸ∂»œÚ◊Û‘À∂Ø£¨µΩ¥Ôµ„
∏ˆµ•Œª√ø√εƒÀŸ∂»œÚ◊Û‘À∂Ø£¨µΩ¥Ôµ„![]() Õ£÷π£Æµ±
Õ£÷π£Æµ±![]() Œ™∫Œ÷µ ±£¨
Œ™∫Œ÷µ ±£¨ ![]() °¢
°¢![]() ∫Õ
∫Õ![]() ÷–«°”–“ª∏ˆµ„Œ™∆‰”ý¡Ωµ„µƒ∫√µ„£ø£®«Î÷±Ω”–¥≥ˆ¥∞∏£©
÷–«°”–“ª∏ˆµ„Œ™∆‰”ý¡Ωµ„µƒ∫√µ„£ø£®«Î÷±Ω”–¥≥ˆ¥∞∏£©


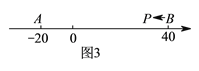
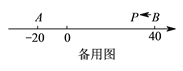
°æ¥∞∏°ø£®1£©![]() ªÚ
ªÚ![]() £ª£®2£©µ±
£ª£®2£©µ±![]() Œ™
Œ™![]() √Σ¨
√Σ¨ ![]() √Σ¨
√Σ¨ ![]() √Î ±£¨
√Î ±£¨ ![]() £¨
£¨ ![]() £¨
£¨ ![]() ÷–«°”–“ª∏ˆµ„Œ™∆‰”ý¡Ωµ„µƒ”≈µ„£Æ
÷–«°”–“ª∏ˆµ„Œ™∆‰”ý¡Ωµ„µƒ”≈µ„£Æ
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©…ËÀ˘«Û ˝Œ™x£¨∏˘æð”≈µ„µƒ∂®“Â∑÷”≈µ„‘⁄M°¢N÷ƺ‰∫Õ”≈µ„‘⁄µ„N”“±þ£¨¡–≥ˆ∑Ω≥ÃΩ‚∑Ω≥ú¥ø…£ª
£®2£©∏˘æð”≈µ„µƒ∂®“Âø…÷™∑÷¡Ω÷÷«Èøˆ£∫¢ŸPŒ™£®A£¨B£©µƒ”≈µ„£ª¢⁄PŒ™£®B£¨A£©µƒ”≈µ„£ª¢€BŒ™£®A£¨P£©µƒ”≈µ„£Æ…˵„P±Ì 浃 ˝Œ™x£¨∏˘æð”≈µ„µƒ∂®“¡–≥ˆ∑Ω≥ã¨Ω¯∂¯µ√≥ˆtµƒ÷µ£Æ
‘Ã‚Ω‚Œˆ£∫£® ![]() £©…ËÀ˘«Û ˝Œ™
£©…ËÀ˘«Û ˝Œ™![]() £¨
£¨
µ±”≈µ„‘⁄![]() £¨
£¨ ![]() ÷ƺ‰ ±£¨”…“‚µ√
÷ƺ‰ ±£¨”…“‚µ√![]() £¨
£¨ ![]() £¨
£¨
µ±”≈µ„‘⁄µ„![]() ”“±þ ±£¨”…“‚µ√
”“±þ ±£¨”…“‚µ√![]() £¨
£¨ ![]() £¨
£¨
π ¥∞∏Œ™![]() ªÚ
ªÚ![]() £Æ
£Æ
£®![]() £©…˵„
£©…˵„![]() ±Ì 浃 ˝Œ™
±Ì 浃 ˝Œ™![]() £¨‘Ú
£¨‘Ú
![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨
£¨
∑÷»˝÷÷«Èøˆ£∫
¢Ÿ![]() Œ™
Œ™![]() µƒ”≈µ„£¨
µƒ”≈µ„£¨
”…“‚µ√£¨ ![]() £¨º¥
£¨º¥![]() £¨
£¨ ![]() £¨
£¨
°ý![]() £®√Σ©£Æ
£®√Σ©£Æ
¢⁄![]() Œ™
Œ™![]() µƒ”≈µ„£¨
µƒ”≈µ„£¨
”…“‚µ√£¨ ![]() £¨º¥
£¨º¥![]() £¨
£¨ ![]() £¨
£¨
°ý![]() £®√Σ©£Æ
£®√Σ©£Æ
¢€![]() Œ™
Œ™![]() µƒ”≈µ„£¨
µƒ”≈µ„£¨
”…“‚µ√![]() £¨º¥
£¨º¥![]() £¨
£¨ ![]() £¨
£¨
¥À ±µ„![]() Œ™
Œ™![]() ÷–µ„£¨º¥
÷–µ„£¨º¥![]() “≤Œ™
“≤Œ™![]() µƒ”≈µ„£¨
µƒ”≈µ„£¨
![]() √Σ¨
√Σ¨
◊€…œÀ˘ ˆ£¨µ±![]() Œ™
Œ™![]() √Σ¨
√Σ¨ ![]() √Σ¨
√Σ¨ ![]() √Î ±£¨
√Î ±£¨
![]() £¨
£¨ ![]() £¨
£¨ ![]() ÷–«°”–“ª∏ˆµ„Œ™∆‰”ý¡Ωµ„µƒ”≈µ„£Æ
÷–«°”–“ª∏ˆµ„Œ™∆‰”ý¡Ωµ„µƒ”≈µ„£Æ

°æƒø°øƒ≥»À»•ÀÆπ˚≈˙∑¢ –≥°≤…π∫∆ªπ˚£¨À˚ø¥÷–¡À![]() £¨
£¨ ![]() ¡Ωº“∆ªπ˚£¨’‚¡Ωº“∆ªπ˚∆∑÷ “ª—˘£¨¡„ €º€∂ºŒ™
¡Ωº“∆ªπ˚£¨’‚¡Ωº“∆ªπ˚∆∑÷ “ª—˘£¨¡„ €º€∂ºŒ™![]() ‘™/«ßøÀ£¨≈˙∑¢º€∏˜≤ªœýÕ¨£Æ
‘™/«ßøÀ£¨≈˙∑¢º€∏˜≤ªœýÕ¨£Æ
![]() º“πÊ∂®£∫≈˙∑¢ ˝¡ø≤ª≥¨π˝
º“πÊ∂®£∫≈˙∑¢ ˝¡ø≤ª≥¨π˝![]() «ßøÀ£¨∞¥¡„ €º€µƒ
«ßøÀ£¨∞¥¡„ €º€µƒ![]() ”≈ªð£ª≈˙∑¢ ˝¡ø≤ª≥¨π˝
”≈ªð£ª≈˙∑¢ ˝¡ø≤ª≥¨π˝![]() «ßøÀ£¨∞¥¡„ €º€µƒ
«ßøÀ£¨∞¥¡„ €º€µƒ![]() ”≈ªð£ª≥¨π˝
”≈ªð£ª≥¨π˝![]() «ßøÀµƒ∞¥¡„ €º€µƒ
«ßøÀµƒ∞¥¡„ €º€µƒ![]() ”≈ªð°£
”≈ªð°£
![]() º“µƒπÊ∂®»Áœ¬±Ì£∫
º“µƒπÊ∂®»Áœ¬±Ì£∫
˝¡ø∑∂Œß£®«ßøÀ£© |
|
|
|
|
º€∏Ò£®‘™£© | ¡„ €º€µƒ | ¡„ €º€µƒ | ¡„ €º€µƒ | ¡„ €º€µƒ |
£®![]() £©»Áπ˚À˚≈˙∑¢
£©»Áπ˚À˚≈˙∑¢![]() «ßøÀ∆ªπ˚£¨‘ÚÀ˚‘⁄
«ßøÀ∆ªπ˚£¨‘ÚÀ˚‘⁄![]() °¢
°¢![]() ¡Ωº“≈˙∑¢∑÷±–Ë“™∂ý…Ÿ‘™£ø
¡Ωº“≈˙∑¢∑÷±–Ë“™∂ý…Ÿ‘™£ø
£®![]() £©»Áπ˚À˚≈˙∑¢
£©»Áπ˚À˚≈˙∑¢![]() «ßøÀ∆ªπ˚
«ßøÀ∆ªπ˚![]() £¨«Îƒ„∑÷±”√∫¨
£¨«Îƒ„∑÷±”√∫¨![]() µƒ¥˙ ˝ Ω±Ì æÀ˚‘⁄
µƒ¥˙ ˝ Ω±Ì æÀ˚‘⁄![]() °¢
°¢![]() ¡Ωº“≈˙∑¢À˘–Ë“™µƒ∑—”√£Æ
¡Ωº“≈˙∑¢À˘–Ë“™µƒ∑—”√£Æ
£®![]() £©œ÷‘⁄À˚“™≈˙∑¢
£©œ÷‘⁄À˚“™≈˙∑¢![]() «ßøÀ∆ªπ˚£¨ƒ„ƒÐ∞Ô÷˙À˚—°‘Ò‘⁄ƒƒº“≈˙∑¢∏¸”≈ªð¬£ø«ÎÀµ√˜¿Ì”…£Æ
«ßøÀ∆ªπ˚£¨ƒ„ƒÐ∞Ô÷˙À˚—°‘Ò‘⁄ƒƒº“≈˙∑¢∏¸”≈ªð¬£ø«ÎÀµ√˜¿Ì”…£Æ