题目内容
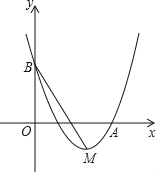
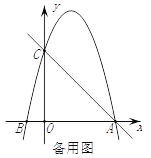
【题目】如图，在平面直角坐标系中，已知点C(0，4)，点A、B在x轴上，并且OA＝OC＝4OB，动点P在过A、B、C三点的抛物线上．
(1)求抛物线的函数表达式；
(2)在直线AC上方的抛物线上，是否存在点P，使得△PAC的面积最大？若存在，求出P点坐标及ΔPAC面积的最大值；若不存在，请说明理由．
(3)在x轴上是否存在点Q，使得△ACQ是等腰三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
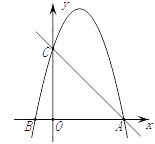
【答案】（1）y＝x2＋3x＋4；(2)存在, 当P点坐标为（2，6）时，ΔPAC面积的最大值是8；（3）Q(0,0),(－4,0),
．
【解析】试题分析：（1）根据点C的坐标，即可求得OC的长，再求得点A、B的坐标，利用待定系数法即可求得函数的解析式；（2）存在，作PN⊥x轴交AC于N，先求得直线AC的解析式，设P（x，x2＋3x＋4），则N(x,－x＋4)，即可得PN＝x2＋4x ，根据三角形的面积公式可得S△PAC＝
PN×4＝－2(x－2)2＋8 ，根据二次函数的性质可得当x=2时，ΔPAC面积的最大值为8，再求得点P的坐标即可；（3）根据勾股定理求得AC=4
，以A为顶点，以AC为腰时，可得AQ=4，此时可得Q的坐标为（4+4，0）、（4-4，0）；以C为顶点，以AC为腰时，AC=AQ,因OC垂直于x轴，可得OA=OQ,此时点Q的坐标为（-4，0）；以O为顶点，以AC为底边时，此时点Q的坐标为（0，0），所以符合条件的点Q的坐标为：(0,0)，(－4,0)，
．
试题解析：
(1)∵C(0,4)，∴OC＝4．
∵OA＝OC＝4OB，∴OA＝4，OB＝1，
∴A(4,0),B(1,0)，
设抛物线解析式：y＝a(x＋1)(x4)，
∴4＝4a，∴a＝1．
∴y＝x2＋3x＋4．
(2)存在．
作PN⊥x轴交AC于N,求得AC的解析式为y＝－x＋4 ，
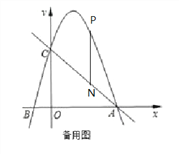
设P（x，x2＋3x＋4），则N(x,－x＋4),
得PN＝（x2＋3x＋4）－(－x＋4)＝x2＋4x ，
∴S△PAC＝PN×4＝2PN＝2(x2＋4x)＝－2(x－2)2＋8 ，
当x=2时，ΔPAC面积的最大值为8，此时点P的坐标为（2，6）.
∴P点坐标为（2，6）时，ΔPAC面积有最大值，最大面积是8 .
(3) 根据勾股定理求得AC=4，分三种情况：
①以A为顶点，以AC为腰时，可得AQ=4，此时可得Q的坐标为（4+4，0）、（4-4，0）；
②以C为顶点，以AC为腰时，AC=AQ,因OC垂直于x轴，可得OA=OQ,此时点Q的坐标为（-4，0）；
③以O为顶点，以AC为底边时，此时点Q的坐标为（0，0），
综上，符合条件的点Q的坐标为：(0,0)，(－4,0)，．
