题目内容
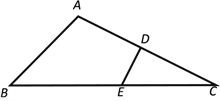
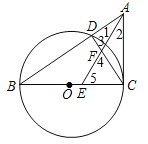
【题目】如图,△ABC中,以BC为直径的⊙O交AB于点D,AE平分∠BAC交BC于点E,交CD于点F.且CE=CF.
(1)求证:直线CA是⊙O的切线;
(2)若BD=![]() DC,求
DC,求![]() 的值.
的值.

【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)若要证明直线CA是⊙O的切线,则只要证明∠ACB=90°即可;
(2)易证△ADF∽△ACE,由相似三角形的性质以及结合已知条件即可求出![]() 的值.
的值.
试题解析:解:(1)证明:∵BC为直径,∴∠BDC=∠ADC=90°,∴∠1+∠3=90°
∵AE平分∠BAC,CE=CF,∴∠1=∠2,∠4=∠5,∴∠2+∠3=90°,∵∠3=∠4,∴∠2+∠5=90°,∴∠ACB=90°,即AC⊥BC,∴直线CA是⊙O的切线;
(2)由(1)可知,∠1=∠2,∠3=∠5,∴△ADF∽△ACE,∴ ![]() ,∵BD=
,∵BD=![]() DC,∴tan∠ABC=
DC,∴tan∠ABC=![]() =
=![]() ,∵∠ABC+∠BAC=90°,∠ACD+∠BAC=90°,∴∠ABC=∠ACD,∴tan∠ACD=
,∵∠ABC+∠BAC=90°,∠ACD+∠BAC=90°,∴∠ABC=∠ACD,∴tan∠ACD=![]() ,∴sin∠ACD=
,∴sin∠ACD=![]() ,∴
,∴![]() =
=![]() .
.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
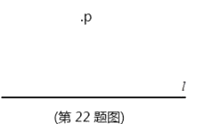
【题目】在数学课上,同学们已经探究过“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
已知:直线
求作:直线 做法:如图:(1)在直线 (2)分别以点 (3)作直线 |
参考以上材料作图的方法,解决以下问题:
(1)以上材料作图的依据是 .
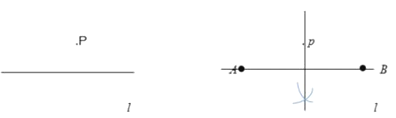
(3)已知:直线![]() 和
和![]() 外一点
外一点![]() ,
,
求作:![]() ,使它与直线
,使它与直线![]() 相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)