题目内容
【题目】如图,在矩形ABCD中,对角线AC、BD相交于点O,AE平分![]() 交BC于点E,若
交BC于点E,若![]() ,
,
(1)求![]() 的度数。
的度数。
(2)求![]() 的度数。
的度数。
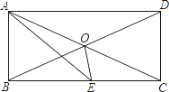
【答案】(1)∠ACB=30°;(2)∠BOE=75°;
【解析】
(1)由矩形的性质可得∠BAD=∠ABC=90°,由角平分线的定义可得∠BAE=45°,从而得∠AEB=45°,再根据三角形外角的性质即可求得答案;
(2)由矩形的性质可得AO=BO=OC,从而有∠OBC=∠OCB=30°,再证明△AOB是等边三角形,从而可得AB=OB,再根据∠BAE=∠AEB=45°,得到AB=BE,继而得BE=BO,再根据等腰三角形的性质即可求得答案.
(1)∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,
∵AE平分∠BAD,
∴∠BAE=45°,
∴∠AEB=90°-∠BAE=45°,
∵∠AEB=∠EAC+∠ACB,∠CAE=15°,
∴∠ACB=45°-15°=30°;
(2)∵四边形ABCD是矩形,
∴AO=CO=![]() AC,BO=
AC,BO=![]() BD,AC=BD,
BD,AC=BD,
∴AO=BO=OC,
∴∠OBC=∠OCB=30°,
∵∠BAO=∠BAE+∠CAE=45°+15°=60°
∴△AOB是等边三角形,
∴AB=OB,
∵∠BAE=∠AEB=45°,
∴AB=BE,
∴BE=BO,
∴∠BOE=(180°-30°)÷2=75°.

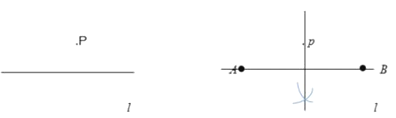
【题目】在数学课上,同学们已经探究过“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
已知:直线
求作:直线 做法:如图:(1)在直线 (2)分别以点 (3)作直线 |
参考以上材料作图的方法,解决以下问题:
(1)以上材料作图的依据是 .
(3)已知:直线![]() 和
和![]() 外一点
外一点![]() ,
,
求作:![]() ,使它与直线
,使它与直线![]() 相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
【题目】某校为了解八年级学生课外阅读情况,随机抽取20名学生平均每周用于课外阅读读的时间(单位:![]() ),过程如下:
),过程如下:
(收集数据)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
(整理数据)
课外阅读时间 |
|
|
|
|
等级 |
|
|
|
|
人数 | 3 |
| 8 |
|
(分析数据)
平均数 | 中位数 | 众数 |
80 |
|
|
请根据以上提供的信息,解答下列问题:
(1)填空:![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)如果每周用于课外读的时间不少于![]() 为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?
为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?