题目内容
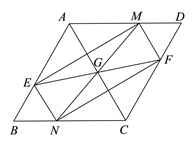
【题目】已知:如图,在□ABCD中,点G为对角线AC的中点,过点G的直线EF分别交边AB、CD于点E、F,过点G的直线MN分别交边AD、BC于点M、N,且∠AGE=∠CGN.

(1)求证:四边形ENFM为平行四边形;
(2)当四边形ENFM为矩形时,求证:BE=BN.
【答案】(1)证明见解析;(2)证明见解析.
【解析】分析:
(1)由已知条件易得∠EAG=∠FCG,AG=GC结合∠AGE=∠FGC可得△EAG≌△FCG,从而可得△EAG≌△FCG,由此可得EG=FG,同理可得MG=NG,由此即可得到四边形ENFM是平行四边形;
(2)如下图,由四边形ENFM为矩形可得EG=NG,结合AG=CG,∠AGE=∠CGN可得△EAG≌△NCG,则∠BAC=∠ACB ,AE=CN,从而可得AB=CB,由此可得BE=BN.
详解:
(1)∵四边形ABCD为平行四四边形边形,
∴AB//CD.
∴∠EAG=∠FCG.
∵点G为对角线AC的中点,
∴AG=GC.
∵∠AGE=∠FGC,
∴△EAG≌△FCG.
∴EG=FG.
同理MG=NG.
∴四边形ENFM为平行四边形.
(2)∵四边形ENFM为矩形,
∴EF=MN,且EG=![]() ,GN=
,GN=![]() ,
,
∴EG=NG,
又∵AG=CG,∠AGE=∠CGN,
∴△EAG≌△NCG,
∴∠BAC=∠ACB ,AE=CN,
∴AB=BC,
∴AB-AE=CB-CN,
∴BE=BN.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目