题目内容
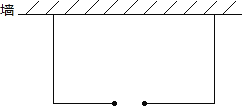
【题目】某商店经销一种学生用双肩包，已知这种双肩包的成本价为每个30元，市场调查发现，这种双肩包每天的销售量(个)与y销售单价x(元)有如下关系:
，设这种双肩包每天的销售利润为w元．
(1)这种双肩包销售单价定为多少元时，每天的销售利润最大?最大利润是多少元?
(2)如果物价部门规定这种双肩包的销售单价不高于42元，该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为多少元?
【答案】（1）当x=45时，w有最大值，最大值是225;（2）获得200元的销售利润，销售单价应定为40元
【解析】
（1）根据销售利润=单件利润
销售量，列出函数关系式，根据二次函数的性质求出最大值即可；
（2）根据二次函数与一元二次方程的关系可计算得，同时要注意考虑实际问题，对答案进行取舍即可．
解:
与
之间的函数解析式
根据题意得: 
w，
∵
，
当x=45时，w有最大值，最大值是225
(2)当
时，
，
解得
，
不符合题意，舍去，
答:该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为40元．
练习册系列答案
相关题目
【题目】某台机床生产铸件产品，按照生产标准，铸件产品评定等级、整改费用规定如下：
重量 （单位： | 评定等级 | 整改费用 （单位：元/件） |
| 特优品 | |
| 优等品 | |
| 合格品 | |
| 不合格品 | 50 |
| 不合格品 | 30 |
注：在统计优等品个数时，将特优品计算在内；在统计合格品个数时，将优等品（含特优品）计算在内.
现该机床生产20件产品，测量其重量，得到如下统计表：
重量 （单位： |
| 29.8 | 29.9 | 30.0 | 30.1 | 30.2 |
|
件数 | 2 | 3 | 4 |
| 3 | 1 |
|
对照生产标准，发现这批铸件产品的合格率为
.
（1）求
与
的值；
（2）根据客户要求，这批铸件产品的合格率不得低于
.现决定从不合格产品中随机抽取两件进行整改，求整改费用最低的概率.
