��Ŀ����
����Ŀ����ͼ��ʾ���ڡ�ABC�У���C��90����AC��5cm��BC��7cm����P�ӵ�A�����ر�AC���C��1cm/s���ٶ��ƶ�����Q��C�������CB�����B��2cm/s���ٶ��ƶ���
��1�����P��Qͬʱ�����������Ӻ�ʹ��PCQ�����Ϊ4cm2��
��2����P��Q���ƶ������У��Ƿ����ijһʱ�̣�ʹ�á�PCQ��������ڡ�ABC�������һ�룿�����ڣ�����˶���ʱ�䣻�������ڣ�˵�����ɣ�
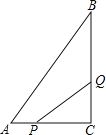
���𰸡���1��1s��2�������ڣ����ɼ�����
��������
��1����P��Qͬʱ������x���Ӻ�AP��xcm��PC����5��x��cm��CQ��2xcm����ʱ��PCQ�����Ϊ��![]() ��2x��5��x�������ʽ��4���ɴ˵�����ϵ�г�����������������ֵ��
��2x��5��x�������ʽ��4���ɴ˵�����ϵ�г�����������������ֵ��
��2�������ABC�������������b2��4ac�ķ��ŵó����ɣ�
�⣺��1����xs��ʹ��PCQ�����Ϊ4cm2��
������ã�AP��xcm��PC����5��x��cm��CQ��2xcm��
��![]() ��5��x��
��5��x��![]() 2x��4��
2x��4��
��������x2��5x+4��0��
���x1��1��x2��4����ȥ����
����P��Qͬʱ������1s���ʹ��PCQ�����Ϊ4cm2��
��2����S��ABC��![]() ��5��7��
��5��7��![]() ��
��
�൱��PCQ��������ڡ�ABC�������һ�룬��S��PCQ��![]() ��
��
��![]() ��5��x��2x��
��5��x��2x��![]() ��
��
�����ã�4x2��20x+35��0��
b2��4ac��400��4��4��35����160��0��
�ʴ˷����⣬���PCQ����������ܵ��ڡ�ABC�������һ�룮