ЬтФПФкШн
ЁОЬтФПЁПФГЬЈЛњДВЩњВњж§МўВњЦЗЃЌАДееЩњВњБъзМЃЌж§МўВњЦЗЦРЖЈЕШМЖЁЂећИФЗбгУЙцЖЈШчЯТЃК
жиСП ЃЈЕЅЮЛЃК | ЦРЖЈЕШМЖ | ећИФЗбгУ ЃЈЕЅЮЛЃКдЊ/МўЃЉ |
| ЬигХЦЗ | |
| гХЕШЦЗ | |
| КЯИёЦЗ | |
| ВЛКЯИёЦЗ | 50 |
| ВЛКЯИёЦЗ | 30 |
зЂЃКдкЭГМЦгХЕШЦЗИіЪ§ЪБЃЌНЋЬигХЦЗМЦЫудкФкЃЛдкЭГМЦКЯИёЦЗИіЪ§ЪБЃЌНЋгХЕШЦЗЃЈКЌЬигХЦЗЃЉМЦЫудкФк.
ЯжИУЛњДВЩњВњ20МўВњЦЗЃЌВтСПЦфжиСПЃЌЕУЕНШчЯТЭГМЦБэЃК
жиСП ЃЈЕЅЮЛЃК |
| 29.8 | 29.9 | 30.0 | 30.1 | 30.2 |
|
МўЪ§ | 2 | 3 | 4 |
| 3 | 1 |
|
ЖдееЩњВњБъзМЃЌЗЂЯжетХњж§МўВњЦЗЕФКЯИёТЪЮЊ![]() .
.
ЃЈ1ЃЉЧѓ![]() гы
гы![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉИљОнПЭЛЇвЊЧѓЃЌетХњж§МўВњЦЗЕФКЯИёТЪВЛЕУЕЭгк![]() .ЯжОіЖЈДгВЛКЯИёВњЦЗжаЫцЛњГщШЁСНМўНјааећИФЃЌЧѓећИФЗбгУзюЕЭЕФИХТЪ.
.ЯжОіЖЈДгВЛКЯИёВњЦЗжаЫцЛњГщШЁСНМўНјааећИФЃЌЧѓећИФЗбгУзюЕЭЕФИХТЪ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() .ЃЈ2ЃЉ
.ЃЈ2ЃЉ![]() ЃЈећИФЗбгУзюЕЭЃЉ
ЃЈећИФЗбгУзюЕЭЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЭГМЦБэжаЕФВњЦЗКЯИёЕФМўЪ§НсКЯВњЦЗЕФКЯИёТЪПЩЕУГіxЕФжЕЃЌНјЖјПЩЕУГіyЕФжЕЃЛ
ЃЈ2ЃЉРћгУСаБэЗЈЛђЛЪїзДЭМЗЈРДЧѓНтМДПЩЃЎ
НтЗЈвЛЃКЃЈ1ЃЉгЩЬтвтЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
ЃЈ2ЃЉМЧЁАжиСПаЁгкЛђЕШгк![]() ЁБЕФСНМўВњЦЗЮЊ
ЁБЕФСНМўВњЦЗЮЊ![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ
МЧЁАжиСПДѓгкЛђЕШгк![]() ЁБЕФСНМўВњЦЗЮЊ
ЁБЕФСНМўВњЦЗЮЊ![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ
ЛЪїзДЭМШчЯТЃК
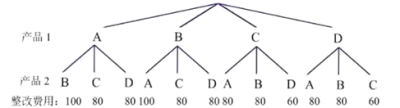
ЫљгаЛњЛсОљЕШЕФНсЙћга12жжЃЌЦфжаећИФЗбгУзюЕЭЕФНсЙћга2жжЃЌ
Ёр![]() ЃЈећИФЗбгУзюЕЭЃЉ
ЃЈећИФЗбгУзюЕЭЃЉ![]() ЃЎ
ЃЎ
НтЗЈЖўЃКЃЈ1ЃЉЭЌНтЗЈвЛЃК
ЃЈ2ЃЉМЧЁАжиСПаЁгкЛђЕШгк![]() ЁБЕФСНМўВњЦЗЮЊ
ЁБЕФСНМўВњЦЗЮЊ![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ
МЧЁАжиСПДѓгкЛђЕШгк![]() ЁБЕФСНМўВњЦЗЮЊ
ЁБЕФСНМўВњЦЗЮЊ![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ
СаБэШчЯТЃК

ЫљгаЛњЛсОљЕШЕФНсЙћга12жжЃЌЦфжаећИФЗбгУзюЕЭЕФНсЙћга2жжЃЌ
ЁрЃЈ![]() ЃЈећИФЗбгУзюЕЭЃЉ
ЃЈећИФЗбгУзюЕЭЃЉ![]() ЃЎ
ЃЎ

 НЬВФШЋНтзжДЪОфЦЊЯЕСаД№АИ
НЬВФШЋНтзжДЪОфЦЊЯЕСаД№АИ