题目内容
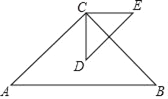
【题目】已知：如图，点D是等腰直角△ABC的重心，其中∠ACB=90°，将线段CD绕点C逆时针旋转90°得到线段CE，连结DE，若△ABC的周长为6，则△DCE的周长为（ ）
A. 2
B. 2
C. 4 D. 3
【答案】A
【解析】
延长CD交AB于F．如图，利用等腰直角三角形的性质和重心的性质得到CF平分AB，CD=2DF，则CF=
AB=
CA，所以CD=
CA，再利用旋转的性质可判断△CDE为等腰直角三角形，于是可判定△CDE∽△CAB，然后根据相似三角形的性质计算△CDE的周长．
解：延长CD交AB于F．如图，
∵点D是等腰直角△ABC的重心，
∴CF平分AB，CD=2DF，
∴CF=AB=
CA=CA，
∴CD=
CF=CA，
∵线段CD绕点C逆时针旋转90°得到线段CE，
∴CD=CE，∠DCE=90°，
∴△CDE为等腰直角三角形，
∴△CDE∽△CAB，
∴△CDE的周长：△CAB的周长=CD：CA=，
∴△CDE的周长=×6=2
．
故选：A．
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
