题目内容
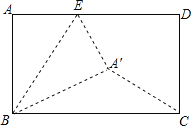
【题目】如图,长方形ABCD中,∠A=∠ABC=∠BCD=∠D=90°,AB=CD=6,AD=BC=10,点E为射线AD上的一个动点,若△ABE与△A′BE关于直线BE对称,当△A′BC为直角三角形时,AE的长为______.
【答案】2或18
【解析】
分两种情况:点E在AD线段上,点E为AD延长线上的一点,进一步分析探讨得出答案即可.
解:①如图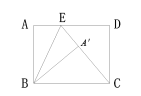
点E在AD线段上,![]() △ABE与△A′BE关于直线BE对称,
△ABE与△A′BE关于直线BE对称,
![]() △A′BE≌△ABE,
△A′BE≌△ABE,
![]() ∠B A′E=∠A=90
∠B A′E=∠A=90![]() ,AB=A′B
,AB=A′B
![]() ∠B A′C =90
∠B A′C =90![]() ,
,![]() E、A',C三点共线,
E、A',C三点共线,
在△ECD与△CB A′中,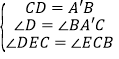 ,
,
![]() △ECD≌△CB A′,
△ECD≌△CB A′,
![]() CE=BC=10,
CE=BC=10,
在RT△CB A′中,A′C=![]() =
=![]() =8,
=8,
![]() AE= A′E=CE- A′C=10-8=2;
AE= A′E=CE- A′C=10-8=2;
②如图
点E为AD延长线上,由题意得:
∠A"BC+∠A"CB=∠DCE+∠A"CB=90![]()
![]() ∠A"BC=∠DCE,
∠A"BC=∠DCE,
在△A"BC与△DCE中,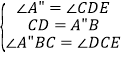
![]() △A"BC≌△DCE,DE= A"C,
△A"BC≌△DCE,DE= A"C,
在RT△ A"BC中,A"C=![]() =
=![]() =8,
=8,
![]() AE=AD+DE=AD+ A"C=10+8=18;
AE=AD+DE=AD+ A"C=10+8=18;
综上所知,AE=2或18.
故答案为:2或18.

练习册系列答案
相关题目