题目内容
【题目】如图,在△ABC中,AB=AC,DE垂直平分AB.若BE⊥AC,AF⊥BC,垂足分别为点E,F,连接EF,则∠EFC=_____.
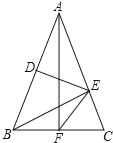
【答案】45°.
【解析】
先根据线段垂直平分线的性质及BE⊥AC得出△ABE是等腰直角三角形,再由等腰三角形的性质得出∠ABC的度数,由AB=AC,AF⊥BC,可知BF=CF,BF=EF;根据三角形外角的性质即可得出结论.
∵DE垂直平分AB,∴AE=BE.
∵BE⊥AC,∴△ABE是等腰直角三角形,∴∠BAC=∠ABE=45°.
又∵AB=AC,∴∠ABC![]() (180°﹣∠BAC)
(180°﹣∠BAC)![]() (180°﹣45°)=67.5°,∴∠CBE=∠ABC﹣∠ABE=67.5°﹣45°=22.5°.
(180°﹣45°)=67.5°,∴∠CBE=∠ABC﹣∠ABE=67.5°﹣45°=22.5°.
∵AB=AC,AF⊥BC,∴BF=CF,∴BF=EF;
∴∠BEF=∠CBE=22.5°,∴∠EFC=∠BEF+∠CBE=22.5°+22.5°=45°.
故答案为:45°.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目