题目内容
【题目】如图,将边长为a与b、对角线长为c的长方形纸片![]() ,绕点
,绕点![]() 顺时针旋转
顺时针旋转![]() 得到长方形
得到长方形![]() ,连接
,连接![]() ,则四边形
,则四边形![]() 为梯形,请通过该图验证勾股定理(求证:
为梯形,请通过该图验证勾股定理(求证:![]() ).
).
【答案】详见解析.
【解析】
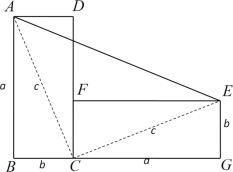
根据S梯形ABEF=S△ABC+S△CEF+S△ACF,利用三角形以及梯形的面积公式即可证明.
解:

证明:∵S梯形ABEF=![]() (EF+AB)BE=
(EF+AB)BE=![]() (a+b)(a+b)=
(a+b)(a+b)=![]() (a+b)2,
(a+b)2,
∵Rt△CDA≌Rt△CGF,
∴∠ACD=∠CFG,
∵∠CFG+∠GCF=90°,
∴∠ACD+∠GCF=90°,
即∠ACF=90°,
∵S梯形ABEF=S△ABC+S△CEF+S△ACF,
∴S梯形ABEF=![]() ab+
ab+![]() ab+
ab+![]() c2,
c2,
∴![]() (a+b)2=
(a+b)2=![]() ab+
ab+![]() ab+
ab+![]() c2
c2
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.

练习册系列答案
相关题目