Question

【题目】已知二次函数y＝ax2－6ax＋5a（a为常数）的图像为抛物线C．

（1）求证：不论a为何值，抛物线C与x轴总有两个不同的公共点；

（2）设抛物线C交x轴于点A、B，交y轴于点D，若△ABD的面积为20，求a的值；

（3）设点E（2，4）、F（3，4），若抛物线C与线段EF只有一个公共点，结合函数图像，直接写出a的取值范围．

Answer 1

【答案】（1）见解析；（2）a＝±2；（3）－≤a≤－1．

【解析】

（1）△=（-6a）2-4a×5a=15a2＞0，即可求解；
（2）△ABD的面积=AB×|yD|=×4×5|a|=20，即可求解；
（3）分a＞0、a＜0两种情况，通过画图找临界点即可求解．

（1）∵二次函数y＝ax2－6ax＋5a，

∴a≠0，
∴△=（-6a）2-4a×5a=15a2＞0，

∴不论a为何值，抛物线C与x轴总有两个不同的公共点；

（2）解：∵ 当x＝0时，y＝5a．

∴ D（0，5a），

当y=0，时x=1或5，

∴A、B的坐标为（1，0），（5，0），

由（1）得，AB＝5－1＝4．

∵△ABD的面积为20，

∴×4×|5a|＝20，

解得 a＝±2．

（3）①当a＞0时，如图1，EF与抛物线不可能有公共点；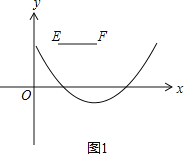

②当a＜0时，如图2，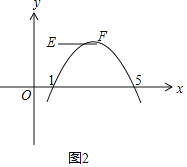

临界点为点E、F，
当抛物线过点E时，即x=2，y=ax2-6ax+5a-3a=-3a=4，解得：a=-，

当抛物线过点F时，即x=3，y=ax2-6ax+5a-3a=-4a=4，解得：a=-1，

∴－≤a≤－1．