题目内容
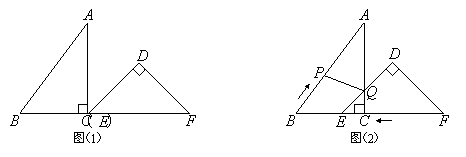
【题目】如图,正方形ABCD的边长是3,点P是直线BC上一点,连接PA,将线段PA绕点P逆时针旋转90°得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF,CF.

(1)如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形;
(2)如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由;
(3)在(2)的条件下,四边形PCFE的面积是否有最大值?若有,请求出面积的最大值及此时BP长;若没有,请说明理由.
【答案】(1)详见解析(2)详见解析(3)有,当BP=![]() 时,最大值为
时,最大值为![]()
【解析】
(1)由正方形的性质可以得出AB=BC,∠ABP=∠ABC=∠90°,可以得出△PBA≌△FBC,由其性质就可以得出结论.
(2)由正方形的性质可以得出AB=BC,∠FBC=∠ABC=∠90°,可以得出△PBA≌△FBC,由其性质就可以得出结论.
(3)设BP=x,则PC=3﹣x 平行四边形PEFC的面积为S,由平行四边形的面积公式就可以求出其解析式,再根据二次函数的性质就可以求出其最大值.
解:(1)∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠PBA=90°
∵在△PBA和△FBC中,AB=BC,∠PBA=∠FBC,BP=BF,
∴△PBA≌△FBC(SAS).∴PA=FC,∠PAB=∠FCB.
∵PA=PE,∴PE=FC.
∵∠PAB+∠APB=90°,∴∠FCB+∠APB=90°.
∵∠EPA=90°,∴∠APB+∠EPA+∠FPC=180°,即∠EPC+∠PCF=180°.
∴EP∥FC,∴四边形EPCF是平行四边形.
(2)结论:四边形EPCF是平行四边形,理由如下:
∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠CBF=90°.
∵在△PBA和△FCB中,AB=BC,∠PBA=∠FBC,BP=BF,
∴△PBA≌△FBC(SAS).∴PA=FC,∠PAB=∠FCB.
∵PA=PE,∴PE=FC.
∵∠FCB+∠BFC=90°,∠EPB+∠APB=90°,∴∠BPE=∠FCB.
∴EP∥FC,∴四边形EPCF是平行四边形.
(3)有.
设BP=x,则PC=3﹣x ,平行四边形PEFC的面积为S,
![]() .
.
∵a=﹣1<0,∴抛物线的开口向下,
∴当x=![]() 时,S最大=
时,S最大=![]() .
.
∴当BP=![]() 时,四边形PCFE的面积最大,最大值为
时,四边形PCFE的面积最大,最大值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某水果店计划购进甲、乙两种高档水果共400千克,每千克的售价、成本与购进数量(千克)之间关系如表:
每千克售价(元) | 每千克成本(元) | |
甲 | ﹣0.1x+100 | 50 |
乙 | ﹣0.2x+120(0<x≤200) | 60 |
|
(1)若甲、乙两种水果全部售完,求水果店获得总利润y(元)与购进乙种水果x(千克)之间的函数关系式(其他成本不计);
(2)若购进两种水果都不少于100千克,当两种水果全部售完,水果能获得的最大利润.