题目内容
【题目】(1)观察下列图形与等式的关系,并填空:
第一个图形: ;
;
第二个图形: ;
;
第一个等式:9+4=13;第二个等式:13+8=21;
第三个图形: ;……;
;……;
第三个等式: + = ;……;
(2)根据以上图形与等式的关系,请你猜出第n个等式(用含有n的代数式表示),并证明.
【答案】(1)17,12,29;(2)(4n+5)+4n=8n+5,证明见解析
【解析】
(1)观察图形的变化写出前两个个图形与等式的关系,进而可得第三个等式;
(2)结合(1)总结规律即可得第n个等式.
解:(1)观察图形的变化可知:
第一个图形:9+4=13,即4×1+5+4=13=8×1+5,
第二个图形:13+8=21,即4×2+5+4×2=21=8×2+5,
第三个图形:17+12=29,即4×3+5+4×3=29=8×3+5,
…
发现规律:
第n个等式为:(4n+5)+4n=8n+5;
故答案为:17,12,29;
(2)由(1)发现的规律:
所以第n个等式为:(4n+5)+4n=8n+5;
证明:左边=4n+5+4n=8n+5=右边.
所以等式成立.

【题目】今年在2月27日国务院对外新闻发布会上,中国疾控中心发言人提到:“在新冠肺炎低风险区域出行仍需戴口罩.”某单位复工,采购了一批医用外科口罩,单价分别为1元、1.5元、3元、5元、10元,每天随机配发给每位在岗员工一个口罩.现将连续10天口罩配发量的情况制成如下统计表.
配发量/个 | 30 | 25 | 20 | 15 |
天数/天 | 2 |
|
| 1 |
已知配发量的平均数是23个,中位数是![]() 个,众数是
个,众数是![]() 个.
个.
(1)求![]() 的值,并计算
的值,并计算![]() ;
;
(2)将配发15个口罩那一天中不同型号的口罩发放情况进行统计,绘制成如图所示的尚不完整的统计图.补全统计图,并求小李当天获得不低于3元口罩的概率;
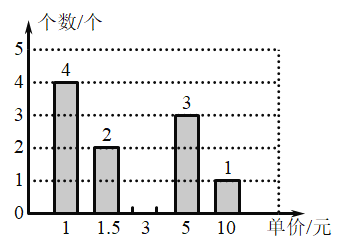
(3)若继续发放两天口罩,且这12天口罩配发量的众数与前10天口罩配发量的众数不同(例如:只要在第11天,第12天都发放30个口罩,则这12天口罩发放量的众数为30个和20个),写出这12天口罩配发量的众数(括号内示例情况不必再述).
【题目】某水果店计划购进甲、乙两种高档水果共400千克,每千克的售价、成本与购进数量(千克)之间关系如表:
每千克售价(元) | 每千克成本(元) | |
甲 | ﹣0.1x+100 | 50 |
乙 | ﹣0.2x+120(0<x≤200) | 60 |
|
(1)若甲、乙两种水果全部售完,求水果店获得总利润y(元)与购进乙种水果x(千克)之间的函数关系式(其他成本不计);
(2)若购进两种水果都不少于100千克,当两种水果全部售完,水果能获得的最大利润.
