题目内容
如图,已知Rt△ABC中,∠A=30°,AC=6,边长为4的等边△DEF沿射线AC运动(A、D、E、C四点共线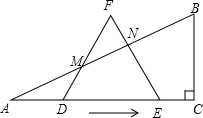 ),使边DF、EF与边AB分别相交于点M、N(M、N不与A、B重合).
),使边DF、EF与边AB分别相交于点M、N(M、N不与A、B重合).(1)求证:△ADM是等腰三角形;
(2)设AD=x,△ABC与△DEF重叠部分的面积为y,求y关于x的函数解析式,并写出x的取值范围;
(3)是否存在一个以M为圆心,MN为半径的圆与边AC、EF同时相切?如果存在,请求出圆的半径;如果不存在,请说明理由.
分析:(1)本题主要通过等角对等边来解决的.
(2)此题的关键是通过解直角三角形求出直角△FMN的MN和FN(用含X的表达式表示出来),从而得出△FMN的面积,再用△FDE的面积减△FMN得面积就得出了Y的面积表达式.注意两种情况.
(3)此题主要通过找出一个简单的等量关系列出方程从而解决问题.
(2)此题的关键是通过解直角三角形求出直角△FMN的MN和FN(用含X的表达式表示出来),从而得出△FMN的面积,再用△FDE的面积减△FMN得面积就得出了Y的面积表达式.注意两种情况.
(3)此题主要通过找出一个简单的等量关系列出方程从而解决问题.
解答:解:(1)证明:

∵△DEF是等边三角形,
∴∠FDE=60°,
∴∠AMD=∠FDE-∠A=30°,
∴∠AMD=∠A,
∴DM=DA,
∴△ADM是等腰三角形.(4分)
(2)解:∵△ADM是等腰三角形,

∴DM=AD=x,FM=4-x,
又∵∠FED=60°,∠A=30°,
∴∠FNM=90°,
∴MN=MF•sinF=(4-x)•
=
(4-x),
FN=
MF=
(4-x).
y=S△FMN=
MN•FN=
•
(4-x)•
(4-x)=
(4-x)2.(5分)
当0<x≤2时,
y=S四边形DENM=S△FDE-S△FMN=4
-
(4-x)2=-
x2+
x+2
.(7分)
当2≤x<4时,
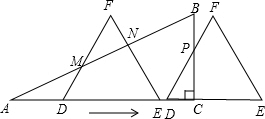
CD=6-x,
∵∠BCE=90°,∠PDC=60°,
∴PC=
(6-x).
∴y=S△PCD=
•
(6-x)•(6-x)=
(6-x)2.
(3)过点M作MG⊥AC于点G,由(2)得DM=x
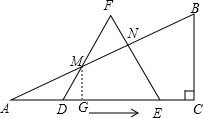
∵∠MDG=60°,
∴MG=
x
∴∠MNF=90°
∴MN⊥FC
要使以点M为圆心,MN长为半径的圆与边AC、EF相切,
则有MG=MN(11分)
即:
x=
(4-x)
解得x=2(12分).
圆的半径MN=
(4-2)=
(13分).
(注:如果学生有不同的解题方法,只要正确,可参考评分标准,酌情给分.)

∵△DEF是等边三角形,
∴∠FDE=60°,
∴∠AMD=∠FDE-∠A=30°,
∴∠AMD=∠A,
∴DM=DA,
∴△ADM是等腰三角形.(4分)
(2)解:∵△ADM是等腰三角形,

∴DM=AD=x,FM=4-x,
又∵∠FED=60°,∠A=30°,
∴∠FNM=90°,
∴MN=MF•sinF=(4-x)•
| ||
| 2 |
| ||
| 2 |
FN=
| 1 |
| 2 |
| 1 |
| 2 |
y=S△FMN=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 8 |
当0<x≤2时,
y=S四边形DENM=S△FDE-S△FMN=4
| 3 |
| ||
| 8 |
| ||
| 8 |
| 3 |
| 3 |
当2≤x<4时,

CD=6-x,
∵∠BCE=90°,∠PDC=60°,
∴PC=
| 3 |
∴y=S△PCD=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
(3)过点M作MG⊥AC于点G,由(2)得DM=x

∵∠MDG=60°,
∴MG=
| ||
| 2 |
∴∠MNF=90°
∴MN⊥FC
要使以点M为圆心,MN长为半径的圆与边AC、EF相切,
则有MG=MN(11分)
即:
| ||
| 2 |
| ||
| 2 |
解得x=2(12分).
圆的半径MN=
| ||
| 2 |
| 3 |
(注:如果学生有不同的解题方法,只要正确,可参考评分标准,酌情给分.)
点评:本题主要考查学生对切线的性质,解直角三角形及二次函数等综合知识的理解掌握及运用的程度.解题的关键是运用数形结合的方法,理解题意,将形的问题利用代数方法去解决.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.
22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.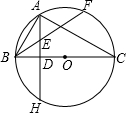 E,交⊙O于点F,且AE=BE.
E,交⊙O于点F,且AE=BE.
 5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.
5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF. 如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.
如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P. 如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为
如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为