题目内容
【题目】尺规作图:过直线外一点作已知直线的平行线.
已知:如图,直线l与直线l外一点P.
求作:过点P与直线l平行的直线.

已知:如图,直线l与直线l外一点P.
求作:过点P与直线l平行的直线.

作法如下:
(1)在直线l上任取两点A、B,连接AP、BP;
(2)以点B为圆心,AP长为半径作弧,以点P为圆心,AB长为半径作弧,如图所示,两弧相交于点M;
(3)过点P、M作直线;
(4)直线PM即为所求.
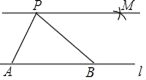
(1)在直线l上任取两点A、B,连接AP、BP;
(2)以点B为圆心,AP长为半径作弧,以点P为圆心,AB长为半径作弧,如图所示,两弧相交于点M;
(3)过点P、M作直线;
(4)直线PM即为所求.

请回答:PM平行于l的依据是_____.
【答案】两组对边分别相等的四边形是平行四边形;平行四边形对边平行;两点确定一条直线.
【解析】
利用画法得到PM=AB,BM=PA,则利用平行四边形的判定方法判断四边形ABMP为平行四边形,然后根据2平行四边形的性质得到PM∥AB.
解:由作法得PM=AB,BM=PA,
∴四边形ABMP为平行四边形,
∴PM∥AB.
故答案为:两组对边分别相等的四边形是平行四边形;平行四边形对边平行;两点确定一条直线.

【题目】体育老师为了解本校九年级女生1分钟“仰卧起坐”体育测试项目的达标情况,从该校九年级136名女生中,随机抽取了20名女生,进行了1分钟仰卧起坐测试,获得数据如下:
收集数据:抽取20名女生的1分钟仰卧起坐测试成绩(个)如下:
38 46 42 52 55 43 59 46 25 38
35 45 51 48 57 49 47 53 58 49
(1)整理、描述数据:请你按如下分组整理、描述样本数据,把下列表格补充完整:
范围 | 25≤x≤29 | 30≤x≤34 | 35≤x≤39 | 40≤x≤44 | 45≤x≤49 | 50≤x≤54 | 55≤x≤59 |
人数 |
|
|
|
|
|
|
|
(说明:每分钟仰卧起坐个数达到49个及以上时在中考体育测试中可以得到满分)
(2)分析数据:样本数据的平均数、中位数、满分率如下表所示:
平均数 | 中位数 | 满分率 |
46.8 | 47.5 | 45% |
得出结论:①估计该校九年级女生在中考体育测试中1分钟“仰卧起坐”项目可以得到满分的人数为 ;
②该中心所在区县的九年级女生的1分钟“仰卧起坐”总体测试成绩如下:
平均数 | 中位数 | 满分率 |
45.3 | 49 | 51.2% |
请你结合该校样本测试成绩和该区县总体测试成绩,为该校九年级女生的1分钟“仰卧起坐”达标情况做一下评估,并提出相应建议.
【题目】一次安全知识测验中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次测验中甲、乙两组学生人数相同,成绩如下两个统计图:
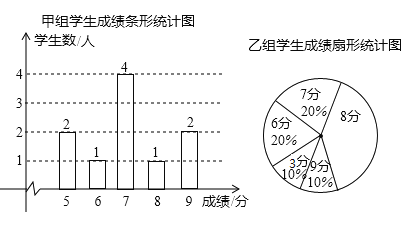
(1)在乙组学生成绩统计图中,8分所在的扇形的圆心角为 度;
(2)请补充完整下面的成绩统计分析表:
平均分 | 方差 | 众数 | 中位数 | 优秀率 | |
甲组 | 7 | 1.8 | 7 | 7 | 20% |
乙组 | 10% |
(3)甲组学生说他们的优秀率高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组学生观点的理由.