Question

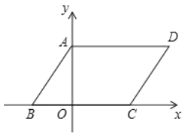
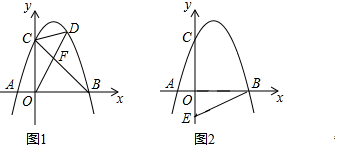
【题目】在平面直角坐标系xOy中，已知A(2t,0)，B(0,-2t)，C(2t,4t)三点，其中t>0，函数的图象分别与线段BC，AC交于点P，Q．若S△PAB-S△PQB=t，则t的值为__．

Answer 1

【答案】4

【解析】

用t分别表示出S△PAB和S△PQB 即可求解.

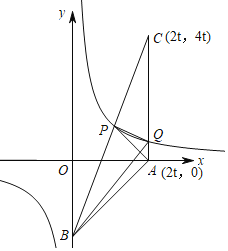
解：如图所示，

∵A（2t，0），C（2t，4t），

∴AC⊥x轴，

当x=2t时，y=，

∴Q（2t，），

∵B（0，﹣2t），C（2t，4t），

易得直线BC的解析式为：y=3x﹣2t，

则3x﹣2t=，

解得：x1=t，x2=（舍），

∴P（t，t），

∵S△PAB=S△BAC﹣S△APC，S△PQB=S△BAC﹣S△ABQ﹣S△PQC，

∵S△PAB﹣S△PQB=t，

∴（S△BAC﹣S△APC）﹣（S△BAC﹣S△ABQ﹣S△PQC）=t，

S△ABQ+S△PQC﹣S△APC=，

t=4，

故答案为：4．