��Ŀ����
����Ŀ����ͼ����֪������m��y=ax2��6ax+c��a��0���Ķ���A��x���ϣ�������B��0��1����ֱ��n��y=�� ![]() x+
x+ ![]() ��x�ύ�ڵ�D����������m�ĶԳ���l���ڵ�F����B���ֱ��BE��ֱ��n�ཻ�ڵ�E����7��7����
��x�ύ�ڵ�D����������m�ĶԳ���l���ڵ�F����B���ֱ��BE��ֱ��n�ཻ�ڵ�E����7��7����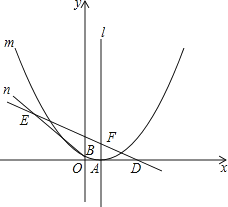
��1����������m�Ľ���ʽ��
��2��P��l�ϵ�һ�����㣬����B��E��PΪ����������ε��ܳ���С�����P�����ꣻ
��3��������m���Ƿ����һ����Q��ʹ���߶�FQΪֱ����Բǡ�þ�����D�������ڣ����Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��������y=ax2��6ax+c��a��0���Ķ���A��x����,
���䷽��y=a��x��3��2��9a+1�����Щ�9a+1=0�����a= ![]()
��A������Ϊ��3��0����������m�Ľ���ʽΪy= ![]() x2��
x2�� ![]() x+1
x+1
��2��
�⣺�ߵ�B���ڶԳ���ֱ��x=3�ĶԳƵ�B��Ϊ��6��1��������EB�佻l�ڵ�P����ͼ��ʾ
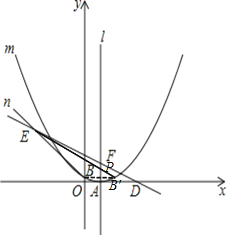
��ֱ��EB��Ľ���ʽΪy=kx+b���ѣ���7��7����6��1�������
![]() ���
��� 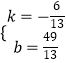 ��
��
��������ʽΪy=�� ![]() x+
x+ ![]()
��x=3������y= ![]() ��
��
���P������3�� ![]() ����
����
��3��
�⣺��y=�� ![]() x+
x+ ![]() ��x�ύ�ڵ�D��
��x�ύ�ڵ�D��
���D������7��0����
��y=�� ![]() x+
x+ ![]() ��������m�ĶԳ���l���ڵ�F��
��������m�ĶԳ���l���ڵ�F��
���F������3��2����
���FD��ֱ�߽���ʽΪy=�� ![]() x+
x+ ![]() ������FQΪֱ����Բ������D���ɵá�FDQ=90�㣬��DQ��ֱ�߽���ʽ��kֵΪ2��
������FQΪֱ����Բ������D���ɵá�FDQ=90�㣬��DQ��ֱ�߽���ʽ��kֵΪ2��
��DQ��ֱ�߽���ʽΪy=2x+b���ѣ�7��0��������b=��14����DQ��ֱ�߽���ʽΪy=2x��14��
���Q������Ϊ��a�� ![]() �����ѵ�Q����y=2x��14��
�����ѵ�Q����y=2x��14��
![]() =2a��14
=2a��14
���a1=9��a2=15��
���Q������9��4����15��16��
����������1�������߶�����x������ɵó�����������Ϊ0��������ʽ�����䷽�Ϳ������a��ֵ���̶��ó���������ʽ����2��������Գ������·���ķ���������ͨ��B�����l�ĶԳƵ�B����ȷ��P��λ�ã������ֱ��B��E�Ľ���ʽ�������ó�P�����ꣻ��3�����������ֱ��FD�Ľ���ʽ��������߶�FQΪֱ����Բǡ�þ�����D�����������ȷ��FDG=90�㣬�ó�ֱ��DG����ʽ��kֵ��ֱ��FD����ʽ��kֵ�˻�Ϊ��1������D���������ֱ��DG����ʽ������Q�����������߽���ʽ��ʾ�����DGֱ�߽���ʽ�������Q���꣮���⿼���֪ʶ���Ƕ��κ������ʡ�һ�κ������ʡ���Գ����ʣ�����Ĺؼ�����ȷ���߶κ���С�ĵ�Ҫͨ����Գ������ҶԳƵ㣬���߶�FQΪֱ����Բǡ�þ�����D��Ҫת��Ϊ��FDG=90������������ǣ�
�����㾫����������Ҫ������һ�κ��������ʺͶ��κ��������ʵ����֪ʶ�㣬��Ҫ����һ��أ�һ�κ���y=kx+b���������ʣ���1����k>0ʱ��y��x�����������2����k<0ʱ��y��x���������С�������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮