题目内容
【题目】已知A,B为抛物线E:y2=2px(p>0)上异于顶点O的两点,△AOB是等边三角形,其面积为48 ![]() ,则p的值为( )
,则p的值为( )
A.2
B.2 ![]()
C.4
D.4 ![]()
【答案】A
【解析】解:设B(x1 , y1),A(x2 , y2), ∵|OA|=|OB|,∴x12+y12=x22+y22 .
又∵y12=2px1 , y22=2px2 ,
∴x22﹣x12+2p(x2﹣x1)=0,
即(x2﹣x1)(x1+x2+2p)=0.
又∵x1、x2与p同号,∴x1+x2+2p≠0.
∴x2﹣x1=0,即x1=x2 .
由抛物线对称性,知点B、A关于x轴对称.
不妨设直线OB的方程为:y= ![]() x,
x,
联立y2=2px,解得B(6p,2 ![]() p).
p).
∵面积为48 ![]() ,
,
∴ ![]() =48
=48 ![]() ,∴p=2
,∴p=2
故选A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】如图①,把∠α=60°的一个单独的菱形称作一个基本图形,将此基本图形不断的复制并平移,使得下一个菱形的一个顶点与前一个菱形的中线重合,这样得到图②,图③,… 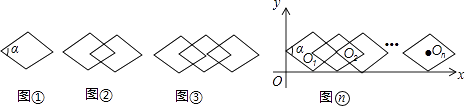
(1)观察以上图形并完成下表:
图形名称 | 基本图形的个数 | 菱形的个数 |
图① | 1 | 1 |
图② | 2 | 3 |
图③ | 3 | 7 |
图④ | 4 | |
… | … | … |
猜想:在图(n)中,菱形的个数为(用含有n(n≥3)的代数式表示);
(2)如图,将图(n)放在直角坐标系中,设其中第一个基本图的对称中心O1的坐标为(x1 , 1),则x1=;第2017个基本图形的中心O2017的坐标为 .