题目内容
【题目】在平面直角坐标系中,A(t,0),B(t+2,0).对于线段AB和点P给出如下定义:当∠APB=90°时,称点P为线段AB的“直角点”.
(Ⅰ)当t=﹣1时,点C(0,1),判断点C是否为线段AB的“直角点”,并说明理由;
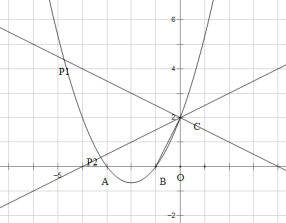
(Ⅱ)已知抛物线y=ax2+bx(a>0,b<0)的顶点为M,与x轴交于A(t,0),B(t+2,0),若点M为线段AB的“直角点”,求出此抛物线的解析式.
【答案】(Ⅰ)C是线段AB的“直角点”,理由见解析;(Ⅱ)y=x2﹣2x.
【解析】
(Ⅰ)t=﹣1时,A(﹣1,0),B(1,0),点C(0,1),即可求解;
(Ⅱ)抛物线y=ax2+bx(a>0,b<0)与x轴交于A(t,0),B(t+2,0),则t=0,即点A、B的坐标分别为:(0,0),(2,0),点M(1,﹣1),即可求解.
(Ⅰ)是,理由:
t=﹣1时,A(﹣1,0),B(1,0),点C(0,1),
则AB=2,AC=![]() ,CB=
,CB=![]() ,
,
则AB2=AC2+BC2,故C是线段AB的“直角点”;
(Ⅱ)抛物线y=ax2+bx(a>0,b<0)与x轴交于A(t,0),B(t+2,0),则t=0,
即点A、B的坐标分别为:(0,0),(2,0),点M(1,﹣1),
AM=![]() ,BM=
,BM=![]() ,AB=2,故点M为线段AB的“直角点”,
,AB=2,故点M为线段AB的“直角点”,
则抛物线的表达式为:y=a(x﹣0)(x﹣2),
将点M坐标代入上式并解得:a=1,
故抛物线的表达式为:y=x2﹣2x.

练习册系列答案
相关题目