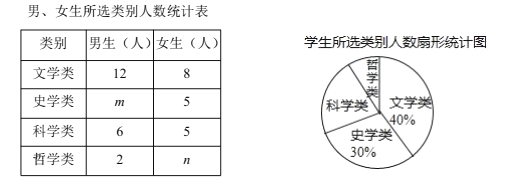
题目内容
【题目】如图,已知将抛物线![]() 沿
沿![]() 轴向上翻折与所得抛物线围成一个封闭区域(包括边界),在这个区域内有5个整点(点
轴向上翻折与所得抛物线围成一个封闭区域(包括边界),在这个区域内有5个整点(点![]() 满足横、纵坐标都为整数,则把点
满足横、纵坐标都为整数,则把点![]() 叫做“整点”).现将抛物线
叫做“整点”).现将抛物线![]() 沿
沿![]() 轴向下翻折,所得抛物线与原抛物线所围成的封闭区域内(包括边界)恰有11个整点,则
轴向下翻折,所得抛物线与原抛物线所围成的封闭区域内(包括边界)恰有11个整点,则![]() 的取值范围是( )
的取值范围是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
画出图象,利用图象可得m的取值范围
解:
∵ ![]()
∴该抛物线开口向下,顶点(-1,2),对称轴是直线x=-1.
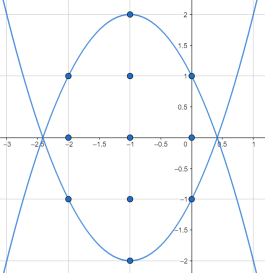
∴点(-1,2)、点(-1,1)、点(-1, 0)、点(-1,-1)、点(-1,-2)符合题意,此时x轴.上的点(-2, 0)、(0, 0)也符合题意,
将(0,1)代入![]() 得到1=a+2.解得a=-1.
得到1=a+2.解得a=-1.
将(1, 0)代入![]() 得到0= 4a+2.解得a=
得到0= 4a+2.解得a=![]()
∵有11个整点,
∴点(0,-1)、点(-2, -1)、点(-2,1)、点(0,1)也必须符合题意.
综上可知:当![]() 时,点(-1,2)、点(-1,1)、点(-1, 0)、点(-1,-1)、点(-1,-2)、点(-2, 0)、(0,0)、点(0,-1)、点(-2,-1)、点(-2,1)、点(0, 1),共有11个整点符合题意,
时,点(-1,2)、点(-1,1)、点(-1, 0)、点(-1,-1)、点(-1,-2)、点(-2, 0)、(0,0)、点(0,-1)、点(-2,-1)、点(-2,1)、点(0, 1),共有11个整点符合题意,
故选: D.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目