题目内容
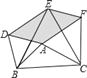
【题目】正方形![]() 中,M为边CB延长线上一点,过点A作直线AM,设∠BAM=α,点B关于直线AM的对称点为点E,连接AE、DE,DE交AM于点N.
中,M为边CB延长线上一点,过点A作直线AM,设∠BAM=α,点B关于直线AM的对称点为点E,连接AE、DE,DE交AM于点N.
(1)依题意补全图形;当α=30°时, 直接写出∠AND的度数;
(2)当α发生变化时,∠AND的度数是否发生变化?说明理由;
(3)探究线段AN,EN,DN的数量关系,并证明.


【答案】(1)∠AND=45 ° ;(2)∠AND的度数不发生变化,理由见解析;(3)DN=![]() .理由见解析.
.理由见解析.
【解析】
(1)依题意补全图形,由正方形的性质得出∠BAD=90°,AB=AD,由轴对称的性质得出AE=AB,∠BAM=∠EAM=α=30°,得出∠EAD=150°,AE=AB=AD,由等腰三角形的性质得出∠AED=∠ADE=15°,即可得出结果;
(2)求出∠EAD=90°+2α.由等腰三角形的性质得出∠AED=∠ADE=45°α.即可得出结果;
(3)过点 A作AG⊥AM,交DE 于点G,连接BN,由轴对称的性质得出AB=AE,∠BAN=∠EAN,证明△ABN≌△AEN得出BN=EN,∠AED=∠ABN,证出∠ABN=∠ADE,得出∠BAN=∠DAG,证明△ABN≌△ADG得出BN=DG,AN=AG,得出△ANG 为等腰直角三角形,EN=BN=DG,即可得出结论.
解:(1)依题意补全图形,如图1所示:
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∵点B关于直线AM的对称点为点E,
∴AE=AB,∠BAM=∠EAM=α=30°,
∴∠EAD=90°+30°+30°=150°,AE=AB=AD,
∴∠AED=∠ADE=![]() (180°150°)=15°,
(180°150°)=15°,
∴∠AND=∠EAN+∠AED=30°+15°=45°;
(2)∠AND的度数不发生变化;
理由如下:
∵∠BAM=∠EAM=α,
∴∠EAD=90°+2α.
∵AE=AB=AD,
∴∠AED=∠ADE=![]() =45°α.
=45°α.
∴∠AND=∠EAN+∠AED=45°α+α=45°;
(3)DN=![]() AN+EN,
AN+EN,
理由如下:
过点 A作AG⊥AM,交DE 于点G,连接BN,如图2所示:
∵点B 与 点E关于直线AM对称,
∴AB=AE,∠BAN=∠EAN,
在△ABN和△AEN中, ,
,
∴△ABN≌△AEN(SAS),
∴BN=EN,∠AED=∠ABN
∵∠AED=∠ADE,
∴∠ABN=∠ADE,
∵∠BAD=∠GAN=90°,
∴∠BAN=∠DAG,
在△ABN和△ADG中, ,
,
∴△ABN≌△ADG(ASA),
∴BN=DG,AN=AG,
∴△ANG 为等腰直角三角形,EN=BN=DG,
∴NG=![]() AN,
AN,
∴DN=![]() AN+EN.
AN+EN.