题目内容
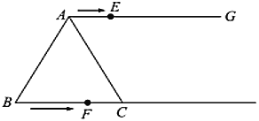
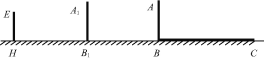
【题目】学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6 m的小明(AB)的影子BC长是3 m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6 m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度GH;
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH的中点B1处时,其影子长为B1C1;当小明继续走剩下路程的![]() 到B2处时,其影子长为B2C2;当小明继续走剩下路程的
到B2处时,其影子长为B2C2;当小明继续走剩下路程的![]() 到B3处,…,按此规律继续走下去,当小明走剩下路程的
到B3处,…,按此规律继续走下去,当小明走剩下路程的![]() 到Bn处时,其影子BnCn的长为
到Bn处时,其影子BnCn的长为![]() m.(直接用含n的代数式表示)
m.(直接用含n的代数式表示)
【答案】(1)详见解析;(2)路灯灯泡的垂直高度GH是4.8 m;(3)BnCn=![]() .
.
【解析】
(1)确定灯泡的位置,可以利用光线可逆可以画出;
(2)要求垂直高度GH可以把这个问题转化成相似三角形的问题,图中△ABC∽△GHC由它们对应成比例可以求出GH;
(3)的方法和(2)一样也是利用三角形相似,对应相等成比例可以求出,然后找出规律.
解:(1)形成影子的光线如图所示,路灯灯泡所在的位置为点G.
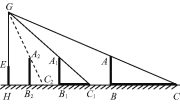
(2)根据题意,得△ABC∽△GHC,∴![]() ,∴
,∴![]() ,解得GH=4.8 m.
,解得GH=4.8 m.
答:路灯灯泡的垂直高度GH是4.8 m.
(3)提示:同理可得△A1B1C1∽△GHC1,∴![]() ,
,
设B1C1长为x m,则![]() ,
,
解得x=1.5,即B1C1=1.5 m.
同理![]() ,解得B2C2=1 m,
,解得B2C2=1 m,
∴![]() ,解得BnCn=
,解得BnCn=![]() .
.

练习册系列答案
相关题目