题目内容
【题目】如图,△ABC 中, AB=11 , AC= 5 ,∠ BAC 的平分线 AD 与边 BC 的垂直平分线 DG 相 交于点 D ,过点 D 分别作 DE⊥AB ,DF⊥AC ,垂足分别为 E 、F,求BE的长度.

【答案】BE=3.
【解析】
连接CD,BD,由角平分线定理得到DF=DE,∠F=∠DEB=90°,∠ADF=∠ADE,由DG是BC的垂直平分线得到CD=BD,由此证明Rt△CDF≌Rt△BDE,推出BE=CF,再根据AB=11 , AC= 5即可求出答案.
如图,连接CD,BD,
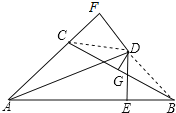
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DF=DE,∠F=∠DEB=90°,∠ADF=∠ADE,
∴AE=AF,
∵DG是BC的垂直平分线,
∴CD=BD,
在Rt△CDF和Rt△BDE中,
![]() ,
,
∴Rt△CDF≌Rt△BDE(HL),
∴BE=CF,
∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE,
∵AB=11,AC=5,
∴BE=![]() ×(11-5)=3.
×(11-5)=3.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目