题目内容
【题目】如图,△ABC为等边三角形,AE=CD,AD交BE于点P.
(1)求证:AD=BE;
(2)设∠BPD=α,那么α的大小是否随D、E的位置变化而变化?

【答案】(1)详见解析;(2)α的大小不随D、E的位置变化.
【解析】
(1)欲证AD=BE,只要证明△ACD≌△BEA即可,根据等边三角形的性质可知AC=AB,∠C=∠BAC,结合已知条件,可利用SAS证得△ACD≌△BEA;
(2)结合(1)由α=∠ABE+∠BAP=∠CAD+∠BAP,即可得出结论.
解:(1)证明:∵△ABC为等边三角形,
∴AC=AB,∠C=∠BAC=60°,
在△ACD和△BAE中,
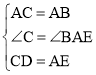 ,
,
∴△ACD≌△BEA(SAS).
∴AD=BE.
(2)不变.
理由:由(1)可知:△ACD≌△BEA,
∴∠CAD=∠ABE,
∵α=∠ABE+∠BAP=∠CAD+∠BAP=60°.
所以α的大小不随D、E的位置变化.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目




