题目内容
梯形ABCD按如图所示放置在直角坐标系中(如图a),AB在x轴上,点D在y轴上,CD∥AB,A(-1,0),C(1,3),抛物线 经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.
经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.(1)求抛物线的解析式与线段BC的长度
(2)当t为何值时,△PHG与△AOD相似(点P与点A对应)?
(3)如图(b),连接AC交y轴于点E,动点Q从点B沿BC以每秒1个单位的速度向终点C运动,设点P、Q同时出发,若其中有一点到达终点,则另一点也立即停止运动.
①请探索:是否存在某一时刻t,使△OPQ是以OP为腰的等腰三角形?若存在,求出此时t的值;若不存在,请说明理由.
②如图(c),连接BD交PQ于F,当t=______
【答案】分析:(1)∵CD∥AB,C(1,3),就可以求出D点的坐标,然后把B、C的坐标代入解析式就可以求出抛物线的解析式.
(2)根据(1)的解析式可以求出顶点G的坐标,从而求出GH,OH进而求出AH的值.利用三角形相似就可以求出PH的值,求出OP的值求出t的值.
(3)①利用等腰三角形的性质,根据3中不同的位置情况,由相似三角形的性质可以求出t的值.
②通过作辅助线证明三角形相似,利用相似三角形的性质对应边成比例可以求出t的值.
解答: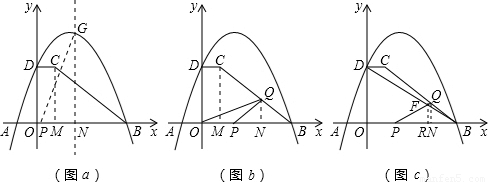
解:(1)∵C(1,3),CD∥AB,
∴D(0,3),
∵A(-1,0),
∴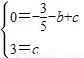
解得 ,
,
抛物线的解析式为:y=- .
.
当y=0时,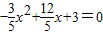 ,
,
解得:x1=-1,x2=5.
过点C作CM⊥AB于M,则CM=DO=3,BM=4,在Rt△MCB中,由勾股定理,得
BC= =5
=5
(2)∵y=- .
.
∴y=-

∴G(2, )
)
∴HG=
当△PHG∽△AOD时, ,
,
∴
∴PH=1.8
∴OP=0.2或OP=3.8,
∴当t=0.2或3.8时,△PHG∽△AOD.
(3)①存在
过点Q作QN⊥AB于N,
∴△BQN∽△BCM
∴得,QN= t,BN=
t,BN= t
t
OQ=OP时,OQ=OP=BQ=t,
∴BN=ON= t,
t,
∴OB= =5,
=5,
∴t=
当OP=PQ时,OP=PQ=BQ=t,
∴MN=PN= t,
t,
∴t+ =5,
=5,
∴t= ,
,
当t=5时,OP=PQ,成立
∴t= 、
、 或5时△OPQ是以OP为腰的等腰三角形.
或5时△OPQ是以OP为腰的等腰三角形.
②分别过点QN⊥AB、FR⊥AB,垂足为N、R.
∴FR∥QN∥OD
∴ ,
,
∴FR=1,BR= ,PR=
,PR= ,PN=5-
,PN=5-
∵FR∥QN,
∴△PRF∽△PNQ
∴ ,
,
∴ ,
,
解得:t= ,
,
∵t=
故答案为: .
.
点评:本题是一道二次函数的综合试题,考查了待定系数法求函数的解析式,勾股定理的运用,等腰三角形的性质,相似三角形的判定及性质.
(2)根据(1)的解析式可以求出顶点G的坐标,从而求出GH,OH进而求出AH的值.利用三角形相似就可以求出PH的值,求出OP的值求出t的值.
(3)①利用等腰三角形的性质,根据3中不同的位置情况,由相似三角形的性质可以求出t的值.
②通过作辅助线证明三角形相似,利用相似三角形的性质对应边成比例可以求出t的值.
解答:

解:(1)∵C(1,3),CD∥AB,
∴D(0,3),
∵A(-1,0),
∴
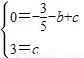
解得
 ,
,抛物线的解析式为:y=-
 .
.当y=0时,
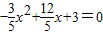 ,
,解得:x1=-1,x2=5.
过点C作CM⊥AB于M,则CM=DO=3,BM=4,在Rt△MCB中,由勾股定理,得
BC=
 =5
=5(2)∵y=-
 .
.∴y=-


∴G(2,
 )
)∴HG=

当△PHG∽△AOD时,
 ,
,∴

∴PH=1.8
∴OP=0.2或OP=3.8,
∴当t=0.2或3.8时,△PHG∽△AOD.
(3)①存在
过点Q作QN⊥AB于N,
∴△BQN∽△BCM
∴得,QN=
 t,BN=
t,BN= t
tOQ=OP时,OQ=OP=BQ=t,
∴BN=ON=
 t,
t,∴OB=
 =5,
=5,∴t=

当OP=PQ时,OP=PQ=BQ=t,
∴MN=PN=
 t,
t,∴t+
 =5,
=5,∴t=
 ,
,当t=5时,OP=PQ,成立
∴t=
 、
、 或5时△OPQ是以OP为腰的等腰三角形.
或5时△OPQ是以OP为腰的等腰三角形.②分别过点QN⊥AB、FR⊥AB,垂足为N、R.
∴FR∥QN∥OD
∴
 ,
,∴FR=1,BR=
 ,PR=
,PR= ,PN=5-
,PN=5-
∵FR∥QN,
∴△PRF∽△PNQ
∴
 ,
,∴
 ,
,解得:t=
 ,
,∵t=

故答案为:
 .
.点评:本题是一道二次函数的综合试题,考查了待定系数法求函数的解析式,勾股定理的运用,等腰三角形的性质,相似三角形的判定及性质.

练习册系列答案
相关题目
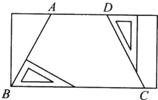 18、在长方形纸上按如图所示的画法,所得梯形ABCD是不是等腰梯形?为什么?
18、在长方形纸上按如图所示的画法,所得梯形ABCD是不是等腰梯形?为什么?

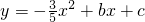 经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.
经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.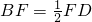 ?(请直接写出答案).
?(请直接写出答案).