题目内容
【题目】如图，四边形ABCD是菱形，点D的坐标是（0， 
），以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A，B两点．
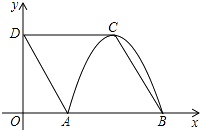
（1）求A，B，C三点的坐标；
（2）求过A，B，C三点的抛物线的解析式；
（3）若将上述抛物线沿其对称轴向上平移后恰好过D点，求平移后抛物线的解析式，并指出平移了多少个单位．
【答案】
（1）
解：过C作CE⊥AB于E，由抛物线的对称性可知AE=BE，
在Rt△AOD和Rt△BEC中，
∵OD=EC，AD=BC，
∴Rt△AOD≌Rt△BEC（HL），
∴OA=BE=AE，（1分）
设菱形的边长为2m，
在Rt△AOD中， 
，
解得m=1；
∴DC=2，OA=1，OB=3；
∴A、B、C三点的坐标分别为（1，0）、（3，0）、（2， 
）
（2）
解：设抛物线的解析式为y=a（x﹣2）2+ ，
代入A点坐标可得a=﹣ ，
抛物线的解析式为y=﹣ （x﹣2）2+
（3）
解：设抛物线的解析式为y=﹣ （x﹣2）2+k，
代入D（0， ）可得k=5 ，
所以平移后的抛物线的解析式为y=﹣ （x﹣2）2+5 ，
向上平移了5 ﹣ =4 个单位．
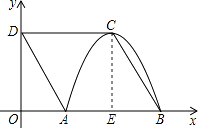
【解析】（1）过C作CE⊥AB于E，根据抛物线的对称性知AE=BE；由于四边形ABCD是菱形，易证得Rt△OAD≌Rt△EBC，则OA=AE=BE，可设菱形的边长为2m，则AE=BE=1m，在Rt△BCE中，根据勾股定理即可求出m的值，由此可确定A、B、C三点的坐标；（2）根据（1）题求得的三点坐标，用待定系数法即可求出抛物线的解析式；（3）设出平移后的抛物线解析式，将D点坐标代入此函数的解析式中，即可求出平移后的函数解析式，与原二次函数解析式进行比较即可得到平移的单位．
【考点精析】通过灵活运用抛物线与坐标轴的交点和菱形的性质，掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．；菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半即可以解答此题．
