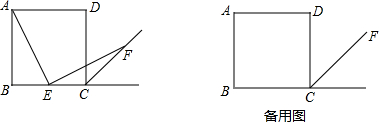题目内容
如图，四边形ABCD是矩形，把这个矩形沿直线AC折叠，点B落在E处．若∠DAC=50°，则∠EAC=
- A.25°
- B.45°
- C.40°
- D.50°
C
分析：根据矩形的四个角都是直角，得∠BAC=40°，再根据折叠的性质即可求解．
解答：∵四边形ABCD是矩形，
∴∠D=90°，
∴∠BAC=40°．
再根据折叠的性质，得∠EAC=∠BAC=40°．
故选C．
点评：此题综合运用了矩形的性质和折叠的性质．
分析：根据矩形的四个角都是直角，得∠BAC=40°，再根据折叠的性质即可求解．
解答：∵四边形ABCD是矩形，
∴∠D=90°，
∴∠BAC=40°．
再根据折叠的性质，得∠EAC=∠BAC=40°．
故选C．
点评：此题综合运用了矩形的性质和折叠的性质．
练习册系列答案
相关题目
如图，四边形ABCD的对角线AC与BD互相垂直平分于点O，设AC=2a，BD=2b，请推导这个四边形的性质．（至少3条）
如图，四边形ABCD的对角线AC、BD交于点P，过点P作直线交AD于点E，交BC于点F．若PE=PF，且AP+AE=CP+CF．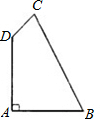
如图，四边形ABCD，AB=AD=2，BC=3，CD=1，∠A=90°，求∠ADC的度数．
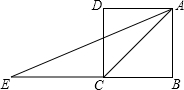如图，四边形ABCD为正方形，E是BC的延长线上的一点，且AC=CE，求∠DAE的度数．