Question

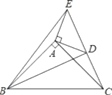
【题目】等腰三角形ABC中，AB=AC，D、E分别是AC、AB上两点，连结BD、CE，BD=CE，且BC>BD，∠A=48°，∠BCE=36°，则∠ADB的度数等于________.

Answer 1

【答案】102°

【解析】

作BG⊥AC于G，作CH⊥AB于H，则∠BHC=∠EHC=∠CGB=∠DGB=90°，由AAS证明△BCH≌△CBG，得出CH=BG，再由HL证明Rt△BDG≌Rt△CEH，得出∠BDG=∠CEH，得出∠ADB=∠AEC，由三角形外角性质求出∠AEC=∠ABC+∠BCE=102°，即可得出结果．

解：作BG⊥AC于点G，作CH⊥AB于点H，如图：

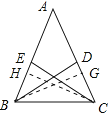
∴∠BHC=∠EHC=∠CGB=∠DGB=90°，

∵AB=AC， ∠A=48°，

∴∠ABC=∠ACB=(180°-∠A)=66°，

在△BCH和△CBG中，

∵，

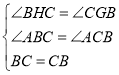∴△BCH≌△CBG(AAS)，

∴CH=BG，

在Rt△BDG和Rt△CEH中，

∵，

∴Rt△BDG≌Rt△CEH(HL)，

∴∠BDG=∠CEH，

∴∠ADB=∠AEC，

∵∠AEC=∠ABC+∠BCE=66°+36°=102°，

∴∠ADB=102°.

故答案为：102°.