��Ŀ����
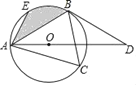
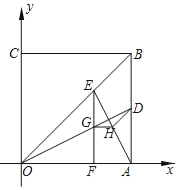
����Ŀ����ͼ��������OABC�Ķ���O��ԭ���غϣ���A��C�ֱ���x����y����������ϣ���A������Ϊ��4��0������D�ڱ�AB�ϣ���tan��AOD��![]() ����E������OB��һ���㣬EF��x���ڵ�F��������OD�ڵ�G������G��GH��x�ύAE�ڵ�H��
����E������OB��һ���㣬EF��x���ڵ�F��������OD�ڵ�G������G��GH��x�ύAE�ڵ�H��
��1����B��D��������ꣻ
��2������E���߶�OB���˶�ʱ�����HDA�Ĵ�С��
��3���Ե�GΪԲ�ģ�GH�ij�Ϊ�뾶����G���Ƿ���ڵ�Eʹ��G��������OABC�ĶԽ������ڵ�ֱ�����У��������ڣ���˵�����ɣ������ڣ���������з��������ĵ�E�����꣮
���𰸡���1��B��4��4����D��4��2������2��45������3�����ڣ����������ĵ�Ϊ��8��4![]() ��8��4
��8��4![]() ����8+4
����8+4![]() ��8+4
��8+4![]() ����
����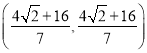 ��
��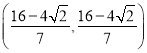 �����ɼ�����
�����ɼ�����
��������
��1��������������֪AB=OA=4����OAB=90�����ݴ˵�B��4��4��������tan��AOD= ![]() ��AD=
��AD=![]() OA=2���ݴ˿ɵõ�D���ꣻ
OA=2���ݴ˿ɵõ�D���ꣻ
��2����![]() ֪GF=
֪GF=![]() OF�����ɡ�AOB=��ABO=45��֪OF=EF����GF=
OF�����ɡ�AOB=��ABO=45��֪OF=EF����GF=![]() EF������GH��x��֪HΪAE���е㣬���DΪAB���е�֪DH����ABE����λ�ߣ���HD��BE���ݴ˿ɵô𰸣�
EF������GH��x��֪HΪAE���е㣬���DΪAB���е�֪DH����ABE����λ�ߣ���HD��BE���ݴ˿ɵô𰸣�
��3���֡�G��Խ���OB�ͶԽ���AC���������������PG=x��������⽨������x�ķ������ɵã�
�⣺��1����A��4��0����
��OA��4��
���ı���OABCΪ�����Σ�
��AB��OA��4����OAB��90����
��B��4��4����
��Rt��OAD����OAD��90����
��tan��AOD��![]() ��
��
��AD��![]() OA��
OA��![]() ��4��2��
��4��2��
��D��4��2����
��2����ͼ1����Rt��OFG�У���OFG��90��
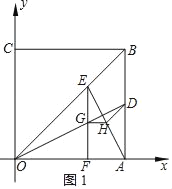
��tan��GOF��![]() ��
��![]() ����GF��
����GF��![]() OF��
OF��
���ı���OABCΪ�����Σ�
���AOB����ABO��45����
��OF��EF��
��GF��![]() EF��
EF��
��GΪEF���е㣬
��GH��x�ύAE��H��
��HΪAE���е㣬
��B��4��4����D��4��2����
��DΪAB���е㣬
��DH����ABE����λ�ߣ�
��HD��BE��
���HDA����ABO��45����
��3��������G��Խ���OB���У�
��ͼ2������E���߶�OB��ʱ��
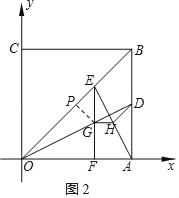
����G��GP��OB�ڵ�P����PG��x���ɵ�PE��x��EG��FG��![]() x��
x��
OF��EF��2![]() x��
x��
��OA��4��
��AF��4��2![]() x��
x��
��GΪEF���е㣬HΪAE���е㣬
��GHΪ��AFE����λ�ߣ�
��GH��![]() AF��
AF��![]() ����4��2
����4��2![]() x����2��
x����2��![]() x��
x��
��x��2��![]() x��
x��
��ã�x��2![]() ��2��
��2��
��E��8��4![]() ��8��4
��8��4![]() ����
����
��ͼ3������E���߶�OB���ӳ�����ʱ��
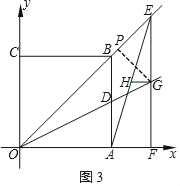
x��![]() x��2��
x��2��
��ã�x��2+![]() ��
��
��E��8+4![]() ��8+4
��8+4![]() ����
����
������G��Խ���AC���У�
��ͼ4������E���߶�BM��ʱ���Խ���AC��OB�ཻ�ڵ�M��
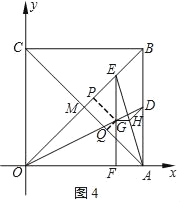
����G��GP��OB�ڵ�P����PG��x���ɵ�PE��x��
EG��FG��![]() x��
x��
OF��EF��2![]() x��
x��
��OA��4��
��AF��4��2![]() x��
x��
��GΪEF���е㣬HΪAE���е㣬
��GHΪ��AFE����λ�ߣ�
��GH��![]() AF��
AF��![]() ����4��2
����4��2![]() x����2��
x����2��![]() x��
x��
����G��GQ��AC�ڵ�Q����GQ��PM��3x��2![]() ��
��
��3x��2![]() ��2��
��2��![]() x��
x��
��![]() ��
��
��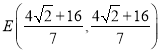 ��
��
��ͼ5������E���߶�OM��ʱ��
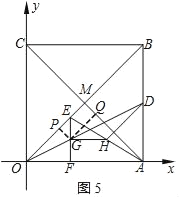
GQ��PM��2![]() ��3x����2
��3x����2![]() ��3x��2��
��3x��2��![]() x��
x��
���![]() ��
��
�� ��
��
��ͼ6������E���߶�OB���ӳ�����ʱ��
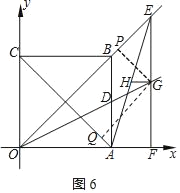
3x��2![]() ��
��![]() x��2��
x��2��
��ã�![]() ����ȥ����
����ȥ����
�������������������ĵ�Ϊ��8��4![]() ��8��4
��8��4![]() ����8+4
����8+4![]() ��8+4
��8+4![]() ����
����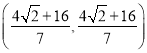 ��
��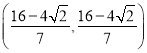 ��
��

 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�