Question

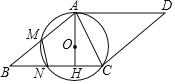
【题目】如图，C是半圆O上一个动点，AB为半圆的直径，D是弧BC的中点，过点D作半圆O的切线DE交AC的延长线于点E．

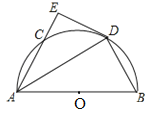
（1）求证：AE⊥DE；

（2）①已知CE=2，DE=4，则AB=　 　；

②连接OC，DC，当∠BAC=　 　度时，四边形OBDC为菱形．

Answer 1

【答案】（1）见解析；（2）①10；②60.

【解析】

（1）连接OD，利用切线的性质和三角形内角和解答即可；

（2）①连接OC、CD、OD，并过点D作AB边上的垂线，垂足为H，利用全等三角形的判定和性质以及勾股定理解答即可；

②利用菱形的性质解答即可．

（1）连接OD．

∵D是弧BC的中点，∴∠EAD=∠DAB．

∵OA=OD，∴∠DAB=∠ADO．

∵∠DAB+∠B=90°，∠ADO+∠ADE=90°，∴∠EDA=∠B，∴∠EAD+∠EDA=90°，∴∠AED=90°，∴AE⊥DE；

（2）①如图，连接OC、CD、OD，并过点D作AB边上的垂线，垂足为H．

∵∠AED=∠AHD=90°，∠EAD=∠DAH，AD=AD，∴△AED≌△AHD（AAS），∴DE=DH=4．

∵D是的中点，∴CD=BD．

∵∠CED=∠BHD=90°，CD=BD，DE=DH，∴Rt△CED≌Rt△BHD（HL），∴CE=HB=2．

在Rt△OHD中，设OD=r，则OH=r﹣2，由勾股定理得：OD2﹣OH2=DH2，即r2﹣（r﹣2）2=42，解得：r=5，∴AB=2r=10；

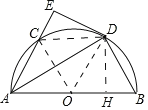
②连接OC，DC，当∠BAC=60度时，四边形OBDC为菱形，理由如下：

∵∠BAC=60°，OA=OC，∴△ACO是等边三角形，∴∠DAB=30°，∴∠B=60°，∴OB=OD=DB，∴OC=OB=BD=CD，∴四边形OBDC是菱形．