题目内容
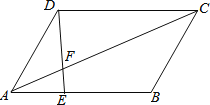
【题目】如图,点![]() 是线段
是线段![]() 上一点,
上一点,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作⊙
的长为半径作⊙![]() ,过点
,过点![]() 作
作![]() 的垂线交⊙
的垂线交⊙![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,以
,以![]() ,
,![]() 为边作
为边作![]() .
.
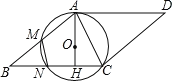
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,求四边形
,求四边形![]() 与⊙
与⊙![]() 重叠部分的面积;
重叠部分的面积;
(3)若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 和
和![]() 的长.
的长.
【答案】(1)见解析;(2) ![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)根据平行四边形的性质可知![]() ,证明
,证明![]() ,又因为
,又因为![]() 为半径,即可证明结论;
为半径,即可证明结论;
(2)利用锐角三角函数先求出![]() ,再求出扇形
,再求出扇形![]() 的面积,最后求出
的面积,最后求出![]() 的面积,两部分面积相加即为重叠部分面积;
的面积,两部分面积相加即为重叠部分面积;
(3)设⊙![]() 半径
半径![]() ,
,![]() ,在
,在![]() 中,利用勾股定理求出半径
中,利用勾股定理求出半径![]() ,推出
,推出![]() ,再在
,再在![]() 和
和![]() 中利用勾股定理分别求出
中利用勾股定理分别求出![]() ,
,![]() 的长,最后证
的长,最后证![]() ,利用相似三角形对应边的比相等即可求出
,利用相似三角形对应边的比相等即可求出![]() 的长.
的长.
(1)证明:![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,即
,即![]() ,
,
又![]()
![]() 为半径,
为半径,
![]()
![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)如图,连接![]() ,
,

![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() 扇形
扇形![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() 四边形
四边形![]() 与⊙
与⊙![]() 重叠部分的面积
重叠部分的面积![]() ;
;
(3)设⊙![]() 半径
半径![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,得
,得![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() 即
即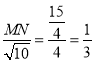 ,
,
![]()
![]() ,
,
![]()
![]() ,
,![]() .
.

练习册系列答案
相关题目
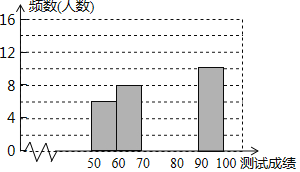
【题目】学校组织“校园诗词大会”,全校学生参加初赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了部分学生的成绩(满分100分),整理得到如下不完整的统计图表:
组别 | 成绩x分 | 频数(人数) | 频率 |
第1组 | 50≤x<60 | 6 | 0.12 |
第2组 | 60≤x<70 | 0.16 | |
第3组 | 70≤x<80 | 14 | a |
第4组 | 80≤x<90 | b | |
第5组 | 90≤x<100 | 10 |
请根据图表中所提供的信息回答下列问题:
(1)统计表中a= ,b= ;
(2)请将统计图表补充完整;
(3)根据调查结果,请估计该校1200名学生中,成绩不低于80分的人数.