题目内容
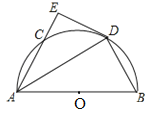
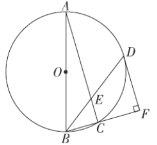
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径作圆,
长为半径作圆,![]() 经过点
经过点![]() ,与
,与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的半径;
的半径;
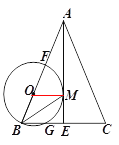
(3)在(2)的条件下,若![]() 的内切圆圆心为
的内切圆圆心为![]() ,直接写出
,直接写出![]() 的长.
的长.
【答案】(1)见解析;(2)20;(3)![]()
【解析】
(1)利用相似三角形的判定定理得到![]() ,从而得到
,从而得到![]() ,根据切线的判定定理证明;(2)过点
,根据切线的判定定理证明;(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,得出四边形
,得出四边形![]() 为矩形,设半径为
为矩形,设半径为![]() ,得出
,得出![]() ,再通过
,再通过![]() ,解方程算出
,解方程算出![]() 的值;(3)根据三角形的面积与三角形内切圆的半径
的值;(3)根据三角形的面积与三角形内切圆的半径![]() 之间满足
之间满足![]() 算出半径,再根据勾股定理计算.
算出半径,再根据勾股定理计算.
(1)证明:
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]()
∴![]() .
.
又∵点![]() 在
在![]() 上,
上,
∴![]() 与
与![]() 相切于点
相切于点![]() .
.
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
∴![]() .
.
在四边形![]() 中,
中,![]() ,
,
∴四边形![]() 为矩形,
为矩形,
∴![]() ,
,![]() ,
,
∴![]() .
.
设![]() 的半径为
的半径为![]() ,则
,则![]() ,
,
∴![]() ,
,![]() .
.
在![]() 和
和![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,即
,即![]() .
.
∴![]() .
.
即![]() 的半径为20.
的半径为20.
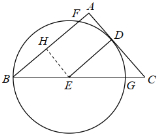
(3)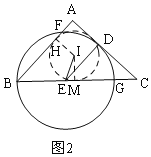
如图2:过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]()
由(2)得:![]()
∴![]()
∵![]() 是
是![]() 的内心
的内心
∵![]()
即![]() 解得:
解得:![]()
∴![]()
∴![]()
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
销售额 |
|
|
|
|
|
|
|
频数 | 7 | 9 | 3 |
| 2 |
| 2 |
数据分析表
平均数 | 众数 | 中位数 |
20.3 |
| 18 |
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.