题目内容
【题目】如图,已知AB=AD,∠BAD=60°,∠BCD=120°,延长BC,使CE=CD,连接DE,求证:BC+DC=AC.
思路点拨: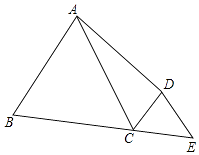
(1)由已知条件AB=AD,∠BAD=60°,可知:△ABD是三角形;
(2)同理由已知条件∠BCD=120°得到∠DCE= , 且CE=CD,可知;
(3)要证BC+DC=AC,可将问题转化为两条线段相等,即=;
请你先完成思路点拨,再进行证明.
【答案】
(1)等边
(2)60°;△CDE为等边三角形
(3)BE;AC
【解析】证明:
连接BD,
∵AB=AD,∠BAD=60°,
∴△ABD为等边三角形,
∵∠BCD=120°,
∴∠DCE=60°,
∵CE=CD,
∴△DCE为等边三角形,
∴AD=BD,CD=ED,∠ADB=∠CDE=60°,
∴∠ADC=∠BDE,
在△ACD和△BED中
∴△ACD≌△BED(SAS),
∴BE=AC,
∵BE=BC+CE=BC+CD,
∴BC+CD=AC.
故答案为:等边;60°;△CED为等边三角形;BE;AC.
连接BD,由条件可分别证明△ABD和△DCE为等边三角形,则可证明△ACD≌△BED,可得AC=BE,则可证明BC+DC=AC.

练习册系列答案
相关题目
【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
(1)求该校八年级的人数占全校总人数的百分率.
(2)求表中A,B的值.
(3)该校学生平均每人读多少本课外书?
图书种类 | 频数 | 频率 |
科普常识 | 840 | B |
名人传记 | 816 | 0.34 |
漫画丛书 | A | 0.25 |
其它 | 144 | 0.06 |