题目内容
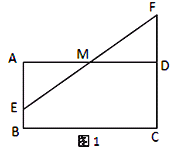
【题目】如图,在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连接EM并延长交线段CD的延长线于点F.
(1)如图1,求证:AE=DF;
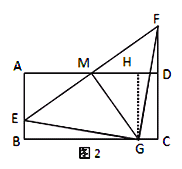
(2)如图2,若AB=2,过点M作 MG⊥EF交线段BC于点G,求证:△GEF是等腰直角三角形
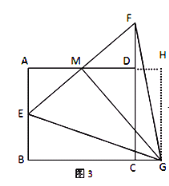
(3)如图3,若AB=2![]() ,过点M作 MG⊥EF交线段BC的延长线于点G.判断△GEF的形状,并说明理由.
,过点M作 MG⊥EF交线段BC的延长线于点G.判断△GEF的形状,并说明理由.

【答案】(1)证明见解析;(2)证明见解析;(3)△GEF是等边三角形.证明见解析.
【解析】试题分析:(1)证明△AEM≌△DFM即可得;
(2)如图2,过点G作GH⊥AD于H,通过证明△AEM≌△HMG从而得出
ME=MG,∠EGM=45°,再由△AEM≌△DFM得ME=MF.从而得到△GEF是等腰直角三角形.
(3)如图3,△GEF是等边三角形.证明△AEM∽△HMG从而得![]() .
.
由tan∠MEG=![]() 得到∠MEG=60°. 由△AEM≌△DFM得到ME=MF.再由MG⊥EF得GE=GF.
得到∠MEG=60°. 由△AEM≌△DFM得到ME=MF.再由MG⊥EF得GE=GF.
从而确定△GEF是等边三角形.
试题解析:(1)如图1,在矩形ABCD中,∠EAM=∠FDM=90°,∠AME=∠FMD.
∵M是AD的中点,∴AM=DM,
∴△AEM≌△DFM(ASA).
∴AE=DF.
(2)如图2,过点G作GH⊥AD于H,
∴∠A=∠B=∠AHG=90°,∴四边ABGH为矩形,∴∠AME+∠AEM=90°,
∵MG⊥EF,∴∠GME=90°,∴∠AME+∠GMH=90°,∴∠AEM=∠GMH.
∵AD=4,M是AD的中点,∴AM=2,
∵四边ABGH为矩形,∴AB=HG=2,∴AM=HG,∴△AEM≌△HMG(AAS).
∴ME=MG,∴∠EGM=45°,
由(1)得△AEM≌△DFM,∴ME=MF.
∵MG⊥EF,∴GE=GF,∴∠EGF=2∠EGM=90°,∴△GEF是等腰直角三角形.
(3)如图3,△GEF是等边三角形.
过点G作GH⊥AD交AD延长线于点H,
∵∠A=∠B=∠AHG=90°,∴四边形ABGH是矩形. ∴GH=AB=![]() .
.
∵MG⊥EF,∴∠GME=90°.∴∠AME+∠GMH=90°.
∵∠AME+∠AEM=90°,∴∠AEM=∠GMH.
又∵∠A=∠GHM=90°,∴△AEM∽△HMG.∴ ![]() .
.
在Rt△GME中,∴tan∠MEG=![]() .
.
∴∠MEG=60°. 由(1)得△AEM≌△DFM.∴ME=MF.∵MG⊥EF, ∴GE=GF.
∴△GEF是等边三角形.

 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案【题目】近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计,以下是本次调查结果的统计表和统计图.
组别 | A | B | C | D | E |
锻炼时间t(分钟) | t<40 | 40≤t<60 | 60≤t<80 | 80≤t<100 | t≥100 |
人数 | 12 | 30 | a | 24 | 12 |
(1)本次被调查的学生数为 人;
(2)统计表中a的值为 ;
(3)扇形统计图中C组所在扇形圆心角为 度;
(4)根据调查结果,请你估计该校1200名学生每天体育锻炼时间不少于1小时的学生人数