ЬтФПФкШн
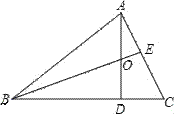
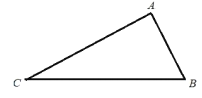
ЁОЬтФПЁПШчЭМ(1), вбжЊЁїABCжа, ЁЯBAC=900, AB=AC, AEЪЧЙ§AЕФвЛЬѕжБЯп, ЧвB.CдкA.EЕФвьВр, BDЁЭAEгкD, CEЁЭAEгкE
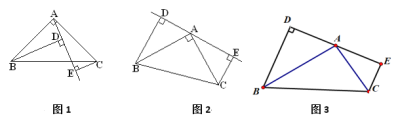
(1)ЪдЫЕУї: BD=DE+CE.
(2)ШєжБЯпAEШЦAЕуа§зЊЕНЭМ(2)ЮЛжУЪБ, ЦфгрЬѕМўВЛБф, ЮЪBDгыDE.CEЕФЪ§СПЙиЯЕШчКЮ?ЧыжБНгаДГіНсЙћ, ВЛашЫЕУї
(3)ШчЭМ(3)ШєНЋЭМЃЈ2ЃЉжаЕФAB=ACИФЮЊЁЯABD=ЁЯABCЦфгрЬѕМўВЛБф, ЮЪADгыAEЕФЪ§СПЙиЯЕШчКЮ? ВЂЫЕУїРэгЩ.
ЁОД№АИЁПЃЈ1ЃЉBD=DE+CEЃЛЃЈ2ЃЉBD=DE-CEЃЛЃЈ3ЃЉAD=AE.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнвбжЊРћгУAASХаЖЈЁїABDЁеЁїCAEЕУГіBD=AEЃЌAD=CEЃЌИљОнЕШСПДњЛЛМДПЩЕУГі.
ЃЈ2ЃЉИљОнвбжЊРћгУAASХаЖЈЁїABDЁеЁїCAEДгЖјЕУЕНBD=AEЃЌAD=CEЃЌгЩAD+AE=BD+CEЃЌЕУГіBDЃЌDEЃЌCEжЎМфЕФЙиЯЕ.
ЃЈ3ЃЉзїAFЁЭBCгкЕуFЃЌЯШИљОнЁАAASЁБжЄУїЁїBADЁеЁїBAFЃЌдйИљОнЁАAASЁБжЄУїЁїCAEЁеЁїCAFЃЌМДПЩЕУЕНADгыAEЕФЪ§СПЙиЯЕ.
НтЃКЃЈ1ЃЉЁпЁЯBAC=90ЁуЃЌBDЁЭAEЃЌCEЁЭAEЃЌ
ЁрЁЯBDA=ЁЯAEC=90ЁуЃЌ
ЁпЁЯABD+ЁЯBAE=90ЁуЃЌЁЯCAE+ЁЯBAE=90Ёу
ЁрЁЯABD=ЁЯCAEЃЌ
ЁпAB=ACЃЌ
дкЁїABDКЭЁїCAEжаЃЌ
Ёп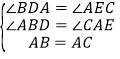 ЃЌ
ЃЌ
ЁрЁїABDЁеЁїCAEЃЈAASЃЉЃЌ
ЁрBD=AEЃЌAD=CEЃЌ
ЁпAE=AD+DEЃЌ
ЁрBD=DE+CEЃЛ
ЃЈ2ЃЉНсТлЃКBD=DE-CEЃЛ
ЁпЁЯBAC=90ЁуЃЌBDЁЭAEЃЌCEЁЭAEЃЌ
ЁрЁЯBDA=ЁЯAEC=90ЁуЃЌ
ЁрЁЯABD+ЁЯDAB=ЁЯDAB+ЁЯCAEЃЌ
ЁрЁЯABD=ЁЯCAEЃЌ
ЁпAB=ACЃЌ
дкЁїABDКЭЁїCAEжаЃЌ
Ёп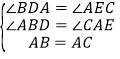 ЃЌ
ЃЌ
ЁрЁїABDЁеЁїCAEЃЈAASЃЉЃЌ
ЁрBD=AEЃЌAD=CEЃЌ
ЁрAD+AE=BD+CEЃЌ
ЁпDE=BD+CEЃЌ
ЁрBD=DE-CEЃЎ
ЃЈ3ЃЉзїAFЁЭBCгкЕуFЃЌ
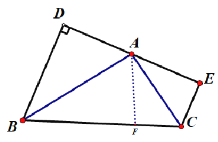
дкЁїBADКЭЁїBAFжаЃЌ
ЁпЁЯABD=ЁЯABCЃЌ
ЁЯD=ЁЯAFBЃЌ
AB=ABЃЌ
ЁрЁїBADЁеЁїBAFЃЌ
ЁрAD=AFЃЌЁЯBAD=ЁЯBAF.
ЁпЁЯCAE+ЁЯBAD=90Ёу, ЁЯCAF+ЁЯBAF=90Ёу,
ЁрЁЯCAE=ЁЯCAF.
дкЁїCAEКЭЁїCAFжаЃЌ
ЁпЁЯCAE=ЁЯCAFЃЌ
ЁЯE=ЁЯAFCЃЌ
AC=ACЃЌ
ЁрЁїCAEЁеЁїCAFЃЌ
ЁрAE=AFЃЌ
ЁрAD=AE.

ЁОЬтФПЁПШЋУёНЁЩэдЫЖЏвбГЩЮЊвЛжжЪБЩа ЃЌЮЊСЫНтНвбєЪаОгУёНЁЩэдЫЖЏЕФЧщПіЃЌФГНЁЩэЙнЕФЙЄзїШЫдБПЊеЙСЫвЛЯюЮЪОэЕїВщЃЌЮЪОэФкШнАќРЈЮхИіЯюФП:
A:НЁЩэЗПдЫЖЏЃЛB:ЬјЙуГЁЮшЃЛC:ВЮМгБЉзпЭХЃЛD:ЩЂВНЃЛE:ВЛдЫЖЏ.
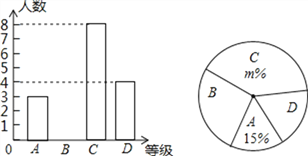
вдЯТЪЧИљОнЕїВщНсЙћЛцжЦЕФЭГМЦЭМБэЕФвЛВПЗжЃЌ
дЫЖЏаЮЪН | A | B | C | D | E |
ШЫЪ§ |
|
|
|
|
|
ЧыФуИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬт:
![]() НгЪмЮЪОэЕїВщЕФЙВга ШЫЃЌЭМБэжаЕФ
НгЪмЮЪОэЕїВщЕФЙВга ШЫЃЌЭМБэжаЕФ![]() ЃЌ
ЃЌ![]() .
.
![]() ЭГМЦЭМжаЃЌ
ЭГМЦЭМжаЃЌ![]() РрЫљЖдгІЕФЩШаЮЕФдВаФНЧЕФЖШЪ§ЪЧ ЖШ.
РрЫљЖдгІЕФЩШаЮЕФдВаФНЧЕФЖШЪ§ЪЧ ЖШ.

![]() НвбєЪаЛЗЕКТЗЪЧЪаУёЯВАЎЕФдЫЖЏГЁЫљжЎвЛЃЌУПЬьЖМгаЁАБЉзпЭХЁБЛюЖЏЃЌШєФГЩчЧјдМга
НвбєЪаЛЗЕКТЗЪЧЪаУёЯВАЎЕФдЫЖЏГЁЫљжЎвЛЃЌУПЬьЖМгаЁАБЉзпЭХЁБЛюЖЏЃЌШєФГЩчЧјдМга![]() ШЫЃЌЧыФуЙРМЦвЛЯТИУЩчЧјВЮМгЛЗЕКТЗЁАБЉзпЭХЁБЕФШЫЪ§.
ШЫЃЌЧыФуЙРМЦвЛЯТИУЩчЧјВЮМгЛЗЕКТЗЁАБЉзпЭХЁБЕФШЫЪ§.