Question

问题探究：
（1）如图①所示是一个半径为

3

2π

，高为4的圆柱体和它的侧面展开图，AB是圆柱的一条母线，一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点，求蚂蚁爬行的最短路程．（探究思路：将圆柱的侧面沿母线AB剪开，它的侧面展开图如图①中的矩形ABB′A′，则蚂蚁爬行的最短路程即为线段AB′的长）；
（2）如图②所示是一个底面半径为

2

3

，母线长为4的圆锥和它的侧面展开图，PA是它的一条母线，一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点，求蚂蚁爬行的最短路程；
（3）如图③所示，在②的条件下，一只蚂蚁从A点出发沿圆锥的侧面爬行一周到达母线PA上的一点，求蚂蚁爬行的最短路程．

Answer 1

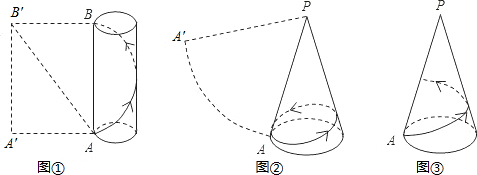
分析：（1）蚂蚁爬行的最短路程为矩形的对角线的长度，由勾股定理可求得．
（2）蚂蚁爬行的最短路程为圆锥展开图中的AA′的连线，可求得△PAA′是等边三角形，则AA′=PA=4．
（3）蚂蚁爬行的最短路程为圆锥展开图中点A到PA的距离．

解答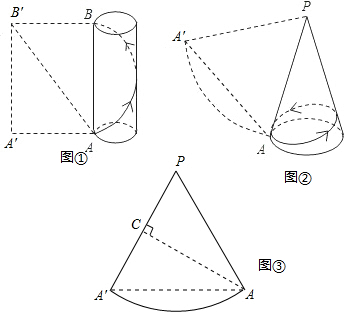：解：（1）∵BB′=2π×

3

2π

=3，
AB′=

AB2+BB′2

=

42+32

=5．
即蚂蚁爬行的最短路程为5．（4分）

（2）连接AA′，则AA′的长为蚂蚁爬行的最短路程，
设r₁为圆锥底面半径，r₂为侧面展开图（扇形）的半径，
则r1=

2

3

，r2=4，
由题意得：2πr1=

nπr2

180

，即2×π×

2

3

=

n

180

×π×4，
∴n=60，
∴△PAA′是等边三角形，
∴最短路程为AA′=PA=4．

（3）如图③所示是圆锥的侧面展开图，
过A作AC⊥PA′于点C，
则线段AC的长就是蚂蚁爬行的最短路程．
∴AC=PA•sin∠APA'=4×sin60°=4×

3

2

=2

3

，
∴蚂蚁爬行的最短距离为2

3

．

点评：本题利用了勾股定理，矩形的性质，圆周长公式，弧长公式，等边三角形的判定和性质，直角三角形的性质求解．