题目内容
问题情境:
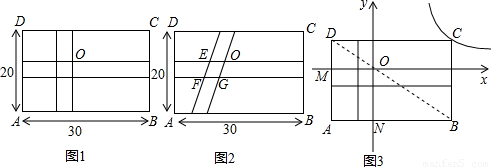
学生生物小组有一块长30m,宽20m的矩形ABCD试验田,为了管理方便,准备沿平行于两边的方向纵、横各开辟一条等宽的小道如图1,要使种植面积为504m2.

问题探究:
(1)如图1,小道的宽应设计为多少m?
(2)若设计者将图1中纵向小道变成如图2所示的一条与横向小道等宽的小道,请你说明两小道重叠部分四边形EFGO是什么特殊的四边形?此时种植面积
(3)若设计者将图1中小道边交叉点O落在矩形ABCD的对角线BD上,并建立如图3所示的直角坐标系,且满足OM=ON,请你求出点A的坐标及过点C的反比例函数的关系式.
学生生物小组有一块长30m,宽20m的矩形ABCD试验田,为了管理方便,准备沿平行于两边的方向纵、横各开辟一条等宽的小道如图1,要使种植面积为504m2.

问题探究:
(1)如图1,小道的宽应设计为多少m?
(2)若设计者将图1中纵向小道变成如图2所示的一条与横向小道等宽的小道,请你说明两小道重叠部分四边形EFGO是什么特殊的四边形?此时种植面积
变化
变化
(填变化或不变)(3)若设计者将图1中小道边交叉点O落在矩形ABCD的对角线BD上,并建立如图3所示的直角坐标系,且满足OM=ON,请你求出点A的坐标及过点C的反比例函数的关系式.
分析:(1)利用把2条道路平移到矩形地块的一边,可得种植面积的形状为一个矩形,根据种植面积为504m2列出方程求解即可;
(2)根据平行四边形以及菱形的判定得出即可,利用纵向小道的底边变大,得出种植面积变化;
(3)利用平行线分线段成比例定理得出
=
,进而求出A点坐标即可,再利用A点坐标,进而得出C点坐标,即可得出答案.
(2)根据平行四边形以及菱形的判定得出即可,利用纵向小道的底边变大,得出种植面积变化;
(3)利用平行线分线段成比例定理得出
| DE |
| NB |
| EO |
| NO |
解答:(1)解:设小道宽为x,
则种植面积(30-x)(20-x)=504,
化简得:x2-50x+96=0,即(x-2)(x-48)=0,
解得:x1=2,x2=48(48>20,故舍去),
答:小道的宽为2米;
(2)两小道重叠部分四边形EFGO是菱形,
证明:如图2,∵四边形EFGO是用等宽的小道交叉重叠地放在一起而组成的图形,
∴EO∥FG,EF∥OG,
∴四边形EFGO是平行四边形(对边相互平行的四边形是平行四边形),
过点G分别作EF,EO边上的高为GN,GJ.
则GN=GJ(两小道宽度相同);
∵平行四边形的面积为:EF×GN=EO×GJ,
∴EF=EO.
∴平行四边形EFGO为菱形(邻边相等的平行四边形是菱形).
∵NG=GJ,NG⊥EF,
∴FG>NG,
∴纵向小道的底边变大,而高不变,此时纵向小道面积增大,
∴此时种植面积变小,
故答案为:变化;
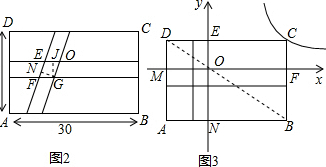
(3)解:如图3,
∵OM=ON,
∴A点横纵坐标相等,设坐标为:(x,x),
则EO=20+x,DE=-x,NO=-x,BN=30+x,
∵DE∥NB,
∴
=
,
∴
=
,
解得:x=-12,
故A点坐标为:A(-12,-12),
∴EC=DC-DE=30-12=18,FC=BC-BF=20-12=8,
故C点坐标为:(18,8),
将C点代入y=
,得:xy=k=18×8=144,
故过点C的反比例函数的关系式为:y=
.
则种植面积(30-x)(20-x)=504,
化简得:x2-50x+96=0,即(x-2)(x-48)=0,
解得:x1=2,x2=48(48>20,故舍去),
答:小道的宽为2米;
(2)两小道重叠部分四边形EFGO是菱形,
证明:如图2,∵四边形EFGO是用等宽的小道交叉重叠地放在一起而组成的图形,
∴EO∥FG,EF∥OG,
∴四边形EFGO是平行四边形(对边相互平行的四边形是平行四边形),
过点G分别作EF,EO边上的高为GN,GJ.
则GN=GJ(两小道宽度相同);
∵平行四边形的面积为:EF×GN=EO×GJ,
∴EF=EO.
∴平行四边形EFGO为菱形(邻边相等的平行四边形是菱形).
∵NG=GJ,NG⊥EF,
∴FG>NG,
∴纵向小道的底边变大,而高不变,此时纵向小道面积增大,
∴此时种植面积变小,
故答案为:变化;

(3)解:如图3,
∵OM=ON,
∴A点横纵坐标相等,设坐标为:(x,x),
则EO=20+x,DE=-x,NO=-x,BN=30+x,
∵DE∥NB,
∴
| DE |
| NB |
| EO |
| NO |
∴
| -x |
| 30+x |
| 20+x |
| -x |
解得:x=-12,
故A点坐标为:A(-12,-12),
∴EC=DC-DE=30-12=18,FC=BC-BF=20-12=8,
故C点坐标为:(18,8),
将C点代入y=
| k |
| x |
故过点C的反比例函数的关系式为:y=
| 144 |
| x |
点评:此题主要考查了一元二次方程的应用以及菱形的判定和平行线分线段成比例定理、反比例函数的性质等知识,根据已知得出A点横纵坐标相等,再利用比例关系求出是解题关键.

练习册系列答案
相关题目