��Ŀ����
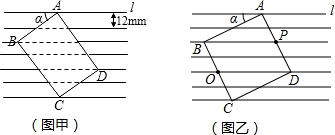
 ��2011•�ٴ���ģ�⣩���ⱳ������ͼ1���ı���ABCD��CEFG���������Σ�B��C��E��ͬһ��ֱ���ϣ�����BG��DE��
��2011•�ٴ���ģ�⣩���ⱳ������ͼ1���ı���ABCD��CEFG���������Σ�B��C��E��ͬһ��ֱ���ϣ�����BG��DE������̽����
��1������ͼ1��ʾ����G��CD����ʱ�������߶�BG��DE��������ϵ������ֱ�ߵ�λ�ù�ϵ������Ҫ��֤����
�ڽ�ͼ1�е�������CEFG���ŵ�C��˳ʱ�루����ʱ�룩������ת����ǶȦ����õ���ͼ2����ͼ3���Σ�����ͨ���۲졢�����ȷ����жϢ��еõ��Ľ����Ƿ���Ȼ��������ѡ��ͼ2��ͼ3֤������жϣ�
������
��2������ԭ���еġ������Ρ���Ϊ�����Ρ�����ͼ4��ʾ������
| AB |
| BC |
| CE |
| CG |
��չӦ�ã�
��3���ڣ�1����ͼ2�У�����DG��BE����AB=3��EF=2����BE2+DG2��ֵ��
��������1��������������ȫ�ȵ��ж����ɵó�BG=DE�������ö�Ӧ�ǹ�ϵ�ó����ɣ�
������������ȫ�ȵ��ж����ɵó�BG=DE�������ö�Ӧ�ǹ�ϵ�ó����ɣ�
��2���������������ε��ж��ó���BCG�ס�DCE�������ó����ɣ�
��3�����ù��ɶ����ó�BE2+DG2=OB2+OE2+OG2+OD2=BD2+GE2�������ó��𰸼��ɣ�
������������ȫ�ȵ��ж����ɵó�BG=DE�������ö�Ӧ�ǹ�ϵ�ó����ɣ�
��2���������������ε��ж��ó���BCG�ס�DCE�������ó����ɣ�
��3�����ù��ɶ����ó�BE2+DG2=OB2+OE2+OG2+OD2=BD2+GE2�������ó��𰸼��ɣ�
��� �⣻��1����BG=DE��BG��DE��
�⣻��1����BG=DE��BG��DE��
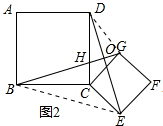
����Ȼ������ѡ��ͼ2֤�����£�
֤�������ı���ABCD��CEFG���������Σ�
��BC=CD��CG=CE����BCD=��ECG��
���BCG=��DCE��
���BCG�ա�DCE��SAS����
��BG=DE����CBG=��CDE��
�֡ߡ�BHC=��DHO����CBG+��BHC=90�㣬
���CDE+��DHO=90�㣬
���DOH=90�㣬
��BG��DE��
��2��BG��DE��
=k��
��ͼ5��
֤����
���ı���ABCD��CEFG���Ǿ��Σ���
=
=k��
��
=
=k����BCD=��ECG=90�㣬
���BCG=��DCE��
���BCG�ס�DCE��
���CBG=��CDE��
=k��
�֡ߡ�BHC=��DHO����CBG+��BHC=90�㣬
���CDE+��DHO=90�㣬
���DOH=90�㣬
��BG��DE��
��3����BG��DE��
��BE2+DG2=OB2+OE2+OG2+OD2=BD2+GE2��
�֡�AB=3��CE=2��
��BD=3
��GE=2
��
��BD2+GE2=��3
��2+��2
��2=26��
��BE2+DG2=26��
 �⣻��1����BG=DE��BG��DE��
�⣻��1����BG=DE��BG��DE������Ȼ������ѡ��ͼ2֤�����£�
֤�������ı���ABCD��CEFG���������Σ�
��BC=CD��CG=CE����BCD=��ECG��
���BCG=��DCE��
���BCG�ա�DCE��SAS����
��BG=DE����CBG=��CDE��
�֡ߡ�BHC=��DHO����CBG+��BHC=90�㣬
���CDE+��DHO=90�㣬
���DOH=90�㣬
��BG��DE��
��2��BG��DE��
| DE |
| BG |
��ͼ5��

֤����
���ı���ABCD��CEFG���Ǿ��Σ���
| AB |
| BC |
| EC |
| CG |
��
| DC |
| BC |
| EC |
| CG |
���BCG=��DCE��
���BCG�ס�DCE��
���CBG=��CDE��
| DE |
| BG |
�֡ߡ�BHC=��DHO����CBG+��BHC=90�㣬
���CDE+��DHO=90�㣬
���DOH=90�㣬
��BG��DE��
��3����BG��DE��
��BE2+DG2=OB2+OE2+OG2+OD2=BD2+GE2��
�֡�AB=3��CE=2��
��BD=3
| 2 |
| 2 |
��BD2+GE2=��3
| 2 |
| 2 |
��BE2+DG2=26��
������������Ҫ������ȫ�������ε��ж��Լ����������ε��ж������ʺ��ɶ�����Ӧ�ã������������������ε����ʵó��ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
 ��2011•�ٴ���ģ�⣩��ͼ������ABCD�У�AB��CD��AD=CD��E��F�ֱ���AB��BC���е㣬����D=108�㣬���1=
��2011•�ٴ���ģ�⣩��ͼ������ABCD�У�AB��CD��AD=CD��E��F�ֱ���AB��BC���е㣬����D=108�㣬���1=