题目内容
(2012•昌平区一模)问题探究:
(1)如图1,在边长为3的正方形ABCD内(含边)画出使∠BPC=90°的一个点P,保留作图痕迹;
(2)如图2,在边长为3的正方形ABCD内(含边)画出使∠BPC=60°的所有的点P,保留作图痕迹并简要说明作法;
(3)如图3,已知矩形ABCD,AB=3,BC=4,在矩形ABCD内(含边)画出使∠BPC=60°,且使△BPC的面积最大的所有点P,保留作图痕迹.

(1)如图1,在边长为3的正方形ABCD内(含边)画出使∠BPC=90°的一个点P,保留作图痕迹;
(2)如图2,在边长为3的正方形ABCD内(含边)画出使∠BPC=60°的所有的点P,保留作图痕迹并简要说明作法;
(3)如图3,已知矩形ABCD,AB=3,BC=4,在矩形ABCD内(含边)画出使∠BPC=60°,且使△BPC的面积最大的所有点P,保留作图痕迹.

分析:(1)正方形对角线的交点符合点P的要求,作对角线即可;
(2)①以BC为边在正方形内作等边△BCQ;
②作△BCQ的外接圆⊙O,分别与AB、DC交于点M、N,由于在⊙O中,弦BC所对
的圆周角均为60°,所
上的所有点均为所求的点P.
(3)以BC为边作等边△BCQ;作等边△QBC的外接圆⊙O与AD交于点 P1、P2,点P1、P2即为所求.
(2)①以BC为边在正方形内作等边△BCQ;
②作△BCQ的外接圆⊙O,分别与AB、DC交于点M、N,由于在⊙O中,弦BC所对
 |
| BQC |
 |
| MN |
(3)以BC为边作等边△BCQ;作等边△QBC的外接圆⊙O与AD交于点 P1、P2,点P1、P2即为所求.
解答: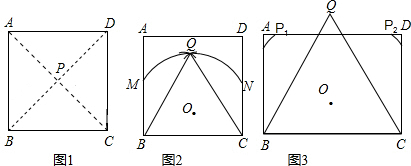 解:(1)如图1,画出对角线AC与BD的交点即为点P.
解:(1)如图1,画出对角线AC与BD的交点即为点P.
注:以BC为直径作上半圆(不含点B、C),则该半圆上的任意一点即可.
(2)如图2,以BC为一边作等边△QBC,作△QBC的外接圆⊙O分别与AB,DC交于点 M、N,弧MN即为点P的集合.
(3)如图3,以BC为一边作等边△QBC,
作△QBC的外接圆⊙O与AD交于点 P1、P2,点P1、P2即为所求.
 解:(1)如图1,画出对角线AC与BD的交点即为点P.
解:(1)如图1,画出对角线AC与BD的交点即为点P. 注:以BC为直径作上半圆(不含点B、C),则该半圆上的任意一点即可.
(2)如图2,以BC为一边作等边△QBC,作△QBC的外接圆⊙O分别与AB,DC交于点 M、N,弧MN即为点P的集合.
(3)如图3,以BC为一边作等边△QBC,
作△QBC的外接圆⊙O与AD交于点 P1、P2,点P1、P2即为所求.
点评:此题主要考查了应用设计与作图,综合利用正方形的性质和同圆中同弧所对的圆周角相等得知识点是解题关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
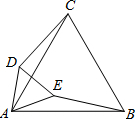 (2012•昌平区一模)如图,已知△ABC和△ADE都是等边三角形,连接CD、BE.求证:CD=BE.
(2012•昌平区一模)如图,已知△ABC和△ADE都是等边三角形,连接CD、BE.求证:CD=BE.