题目内容
如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连接BE交AC于点F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABC;④△ADF与△CFB.其中相似的为
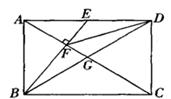
A.①④ B.①② C.②③④ D.①②③

A.①④ B.①② C.②③④ D.①②③
B
试题分析:相似三角形的判定方法:①有两个对应角相等的三角形相似;②有两个对应边的比相等,且其夹角相等,则两个三角形相似;③三组对应边的比相等,则两个三角形相似.
根据题意得:∠BAE=∠ADC=∠AFE=90°
∴∠AEF+∠EAF=90°,∠DAC+∠ACD=90°
∴∠AEF=∠ACD
∴①中两三角形相似;
容易判断△AFE∽△BAE,得
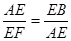
又∵AE=ED,
∴
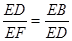
而∠BED=∠BED,
∴△FED∽△DEB.
故②正确;
无法说明③△CFD与△ABC;④△ADF与△CFB相似
故选B.
点评:相似三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
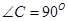 ,AC=8cm,BC=6cm.点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.以AQ、PQ为边作平行四边形AQPD,连接DQ,交AB于点E.设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
,AC=8cm,BC=6cm.点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.以AQ、PQ为边作平行四边形AQPD,连接DQ,交AB于点E.设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:

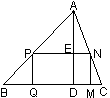

 时,连结C ′C,则以CC´为直径的圆何时与直线AB相切?
时,连结C ′C,则以CC´为直径的圆何时与直线AB相切?