题目内容
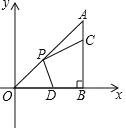
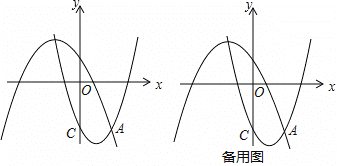
【题目】如图,在平面直角坐标系xOy中,抛物线L1:y=![]() +bx+c过点C(0,3),与抛物线L2:y=
+bx+c过点C(0,3),与抛物线L2:y=![]()
![]() x+2的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、L2上的动点。
x+2的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、L2上的动点。
(1)求抛物线L1对应的函数表达式;
(2)若以点A. C.P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;
【答案】(1)抛物线L1:y=![]() -2x-3;(2)点P的坐标为(-1,0),(3,0)或(-
-2x-3;(2)点P的坐标为(-1,0),(3,0)或(-![]() );
);
【解析】
(1)先求出A点的坐标,再用待定系数法求出函数解析式便可;
(2)设点P的坐标为(x,x2-2x-3),分两种情况讨论:AC为平行四边形的一条边,AC为平行四边形的一条对角线,用x表示出Q点坐标,再把Q点坐标代入抛物线L2:y=![]()
![]() x+2中,列出方程求得解便可.
x+2中,列出方程求得解便可.
(1) 将x=2代入y=![]()
![]() x+2,得y=3,
x+2,得y=3,
故点A的坐标为(2,-3),
将A(2,-1), C(0,3)代入y=![]() +bx+c,
+bx+c,
得-3=![]() +2b+c ,-3=0+0+c,
+2b+c ,-3=0+0+c,
解得b=-2,c=-3,
∴抛物线L1:y=![]() -2x-3;
-2x-3;
(2)设点P的坐标为(x,![]() -2x-3),
-2x-3),
第一种情况:AC为平行四边形的一条边,
①当点Q在点P右侧时,则点Q的坐标为(x+2,![]() -2x-3),
-2x-3),
将Q(x+2,![]() -2x-3)代入y=
-2x-3)代入y=![]()
![]() x+2得,
x+2得,![]() -2x-3=
-2x-3=![]() -
-![]() +2,
+2,
解得,x=0或x=-1,
因为x=0时,点P与C重合,不符合题意,所以舍去,
此时点P的坐标为(-1,0);
②当点Q在点P左侧时,则点Q的坐标为(x-2,![]() -2x-3),
-2x-3),
将Q(x-2,![]() -2x-3)代入y=
-2x-3)代入y=![]()
![]() x+2得,
x+2得,![]() -2x-3=
-2x-3=![]() -
-![]() +2,
+2,
解得,x=3,或x=-![]() ,此时P点的坐标为(3,0)或(-
,此时P点的坐标为(3,0)或(-![]() );
);
第二种情况:当AC为平行四边形的一条对角线时,
由AC的中点坐标为(1,-3),得PQ的中点坐标为(1,-3),
故点Q的坐标为(2-x,-![]() +2x-3),
+2x-3),
将Q(2-x,-![]() +2x-3)代入y=
+2x-3)代入y=![]()
![]() x+2得,-
x+2得,-![]() +2x-3=
+2x-3=![]() -
-![]() +2,
+2,
解得,x=0或x=-3,
因为x=0时,点P与点C重合,不符合题意,所以舍去,
此时点P的坐标为(-3,12),
综上所述,点P的坐标为(-1,0),(3,0)或(-![]() )或(-3,12).
)或(-3,12).

 名校课堂系列答案
名校课堂系列答案