题目内容
【题目】下列命题中错误的命题有( )
①线段垂直平分线上的点与这条线段两端点距离相等;
②若两三角形关于直线L对称,则对应线段所在的直线必相交,且交点在对称轴上;
③顶角和底边对应相等的两个等腰三角形全等;
④一腰和一腰上的高对应相等的两个等腰三角形全等;
⑤有一边上的高也是这边上的中线的等腰三角形是等边三角形
A.1个B.2个C.3个D.4个
【答案】B
【解析】
①根据垂直平分线的性质判断命题的真假;
②根据两个图形成轴对称的知识判断命题的真假;
③④根据证明三角形全等的方法判断命题的真假;
⑤根据等边三角形的证明方法判断命题的真假.
解:线段垂直平分线上的点到线段的两个端点的距离相等,所以命题①是真命题;
若两三角形关于直线L对称,则对应线段所在的直线相交或平行,若对应线段所在的直线相交,且交点在对称轴上,所以命题②是假命题;
顶角相等的两个等腰三角形,三个角都相等,且底边对应相等,则根据ASA或AAS可证这两个等腰三角形全等,所以命题③是真命题;
这两个等腰三角形可分为钝角三角形和锐角三角形来讨论,如下图的甲乙两个等腰三角形:
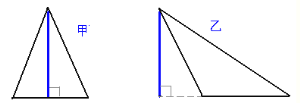
则可知这两个三角形不全等,所以命题④是假命题;
任意等腰三角形底边上的高线也是中线,因此有一边上的高也是这边上的中线的等腰三角形不一定是等边三角形,所以命题⑤是假命题.
故答案选:B.

 名校课堂系列答案
名校课堂系列答案【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?