题目内容
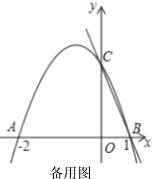
【题目】已知平行四边形![]() 的顶点
的顶点![]() 的坐标分别为
的坐标分别为![]() 顶点在
顶点在![]() 双曲线
双曲线![]()
![]() 上,边
上,边![]() 交
交![]() 轴于点
轴于点![]() .若四边形
.若四边形![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍,则点
倍,则点![]() 的坐标为_________.
的坐标为_________.
【答案】![]()
【解析】
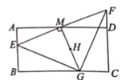
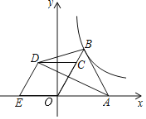
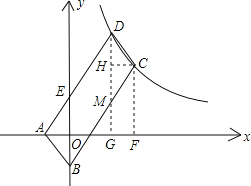
分别过C、D作x轴的垂线,垂足为F、G,过C点作CH⊥DG,垂足为H,根据CD∥AB,CD=AB可证△CDH≌△ABO,则CH=AO=1,DH=OB=2,由此设C(m+1,n),D(m,n+2),C、D两点在双曲线y=上,则(m+1)n=m(n+2),解得n=2m,设直线AD解析式为y=ax+b,将A、D两点坐标代入求解析式,确定E点坐标,求S△ABE,根据S四边形BCDE=5S△ABE,列方程求m、n的值,即可得出点![]() 的坐标.
的坐标.
如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,
∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
在△CDH和△ABO中,
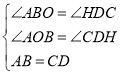 ,
,
∴△CDH≌△ABO(AAS),
∴CH=AO=1,DH=OB=2,
设C(m+1,n),D(m,n+2),
则(m+1)n=m(n+2)=k,
解得n=2m,则D的坐标是(m,2m+2),
设直线AD解析式为y=ax+b,将A、D两点坐标代入得
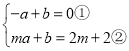 ,
,
由①得:a=b,代入②得:mb+b=2m+2,
即b(m+1)=2(m+1),解得b=2,
∴y=2x+2,
∴E(0,2),BE=4,
∴S△ABE=![]()
∵S四边形BCDE=5S△ABE=5×![]() ×4×1=10,
×4×1=10,
∵S四边形BCDE=S△ABE+S四边形BEDM=10,
即2+4×m=10,
解得:m=2,
∴n=2m=4,
∴点C坐标为(3,4)
故答案为:(3,4).

练习册系列答案
相关题目